The area (in sq. units) of the region
{(x,y):y2≤2xandx2+y2≤4x,x≥0,y≤0},is
A
π−43
B
π−83
C
π−4√23
D
π2−2√23
Video Solution
Text Solution
The correct Answer is:B
The required area A is given by
A=2|y1−y2|0dx
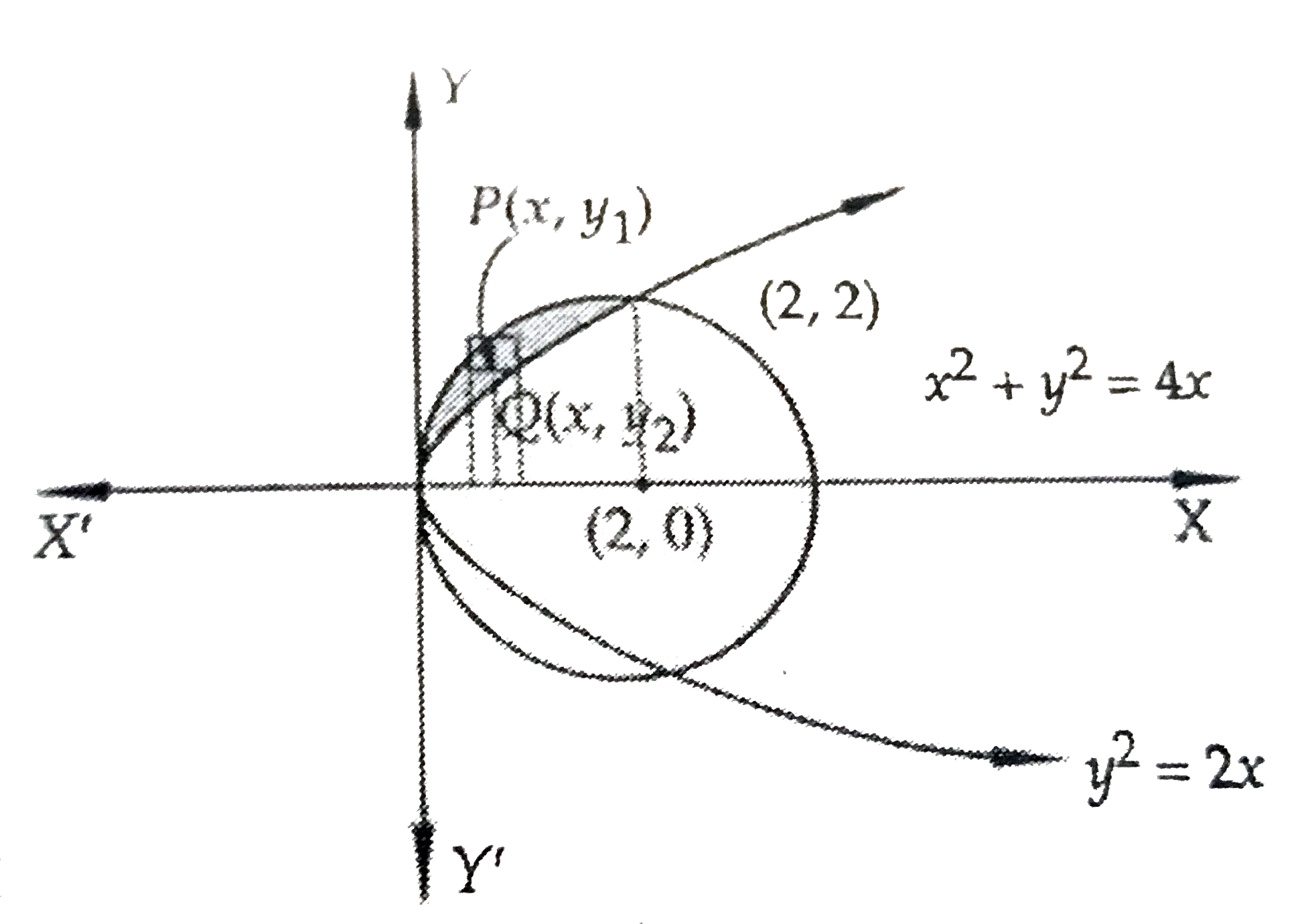
⇒A=2∫0(√4x−x2−√2x)dx
⇒A=2∫0(√22−(x−2)2−√2x)dx
⇒A=[12(x−2)√4x−x2+2sin−1(x−2)22√23x3/2]20
⇒A=−83−2(−π2)=π−83
|
Topper's Solved these Questions
- AREAS OF BOUNDED REGIONSBook:OBJECTIVE RD SHARMAChapter:AREAS OF BOUNDED REGIONSExercise:Exercise
Explore 62 Videos
- AREAS OF BOUNDED REGIONSBook:OBJECTIVE RD SHARMAChapter:AREAS OF BOUNDED REGIONSExercise:Chapter Test
Explore 60 Videos
- APPLICATION OF DERIVATIVESBook:OBJECTIVE RD SHARMAChapter:APPLICATION OF DERIVATIVESExercise:Illustration
Explore 6 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS Book:OBJECTIVE RD SHARMAChapter:CARTESIAN PRODUCT OF SETS AND RELATIONS Exercise:Chapter Test
Explore 31 Videos
Similar Questions
Knowledge Check
The area (in square units) of the region {(x,y):y2≥2xandx2+y2≤4x,x≥0,y≥0} is
Aπ−43Bπ−83Cπ−4√23Dπ2−2√23The area (in sdq. Units) of the region {(x,y):y2≥2x and x2+y2≤4x,x≥0,y≥0} is
Aπ−83Bπ−4√23Cπ2−2√23Dπ−43The area (in sq units) of the region A={(x,y):x2≤y≤x+2} is
A136B92C316D103
The area (in sq units) of the region
A={(x,y):y22≤x≤y+4} is
View SolutionThe area (in square units) of the region described by {(x,y):y2≤2xandy≤4−x} is
View SolutionThe area (in sq units) of the region described by {(x,y):y2≤2xandy≥4x−1} is
View SolutionThe area (in sq. units) of the region, R = {(x,y): y ≤x2,y≤2x+3,x≤1andy+1≥} is :
View SolutionIf the area (in sq. units) of the region {(x,y):y2≤4x,x+y≤1,x≥0,y≥0} is a√2+b, then a−b is equal to :
View Solution

