The area enclosed between the curve y=loge(x+e) and the coordinate axes is
4
3
2
1
The correct Answer is:D
The area enclosed by y=loge(x+e) and the coorcinate axes is shaded in Fig. 17.
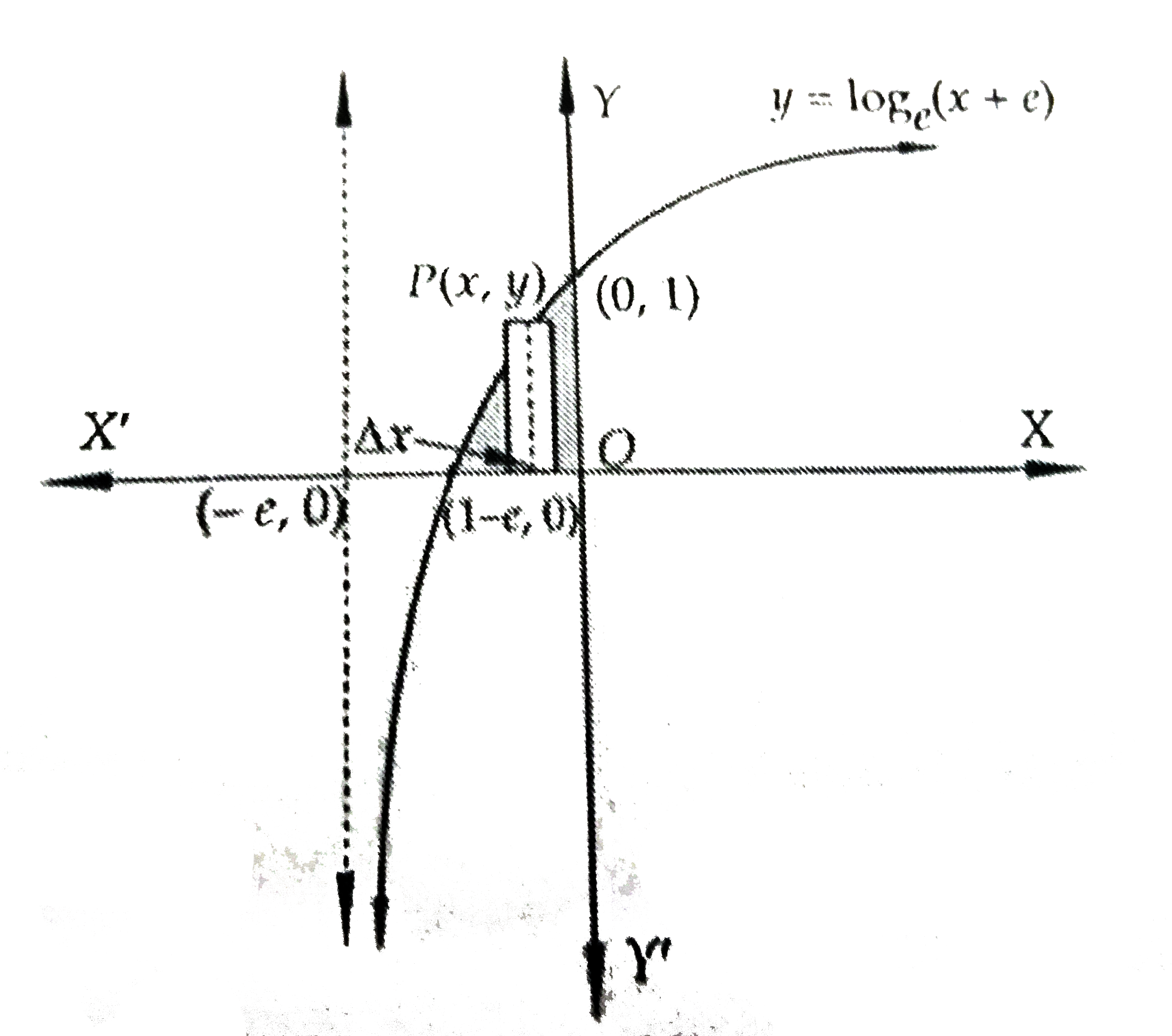
Let A be the required area. Then,
A=0∫1−eydx=0∫1−eloge(x+e)dx
⇒A=[xloge(x+e)]01−e−0∫1−exx+edx
⇒A=[xloge(x+e)]01−e−[x−eloge(x+e)]01−e
⇒A=0−[(0−e)−(1−e)+0]=1 sq. units
Related Playlists
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Exercise61videos
AREAS OF BOUNDED REGIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test60videos
AREAS OF BOUNDED REGIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Exercise39videos
ALGEBRAIC INEQUATIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test30videos
CARTESIAN PRODUCT OF SETS AND RELATIONS
Similar Questions
Find the area enclosed between the curve y=x2 , the axis and the ordinates x = 1 and x=2 .
View SolutionThe area enclosed between the curves y2=xandy=|x| is
View SolutionThe area enclosed by the curve y2+x4=x2 is
View SolutionFind the area enclosed between the curves: y=loge(x+e),x=loge(1y) & the x-axis.
View SolutionThe area enclosed within the curve |x|+|y|=1 is
View SolutionUsing integration, find the area enclosed between the curve y=2x−x2, and the x-axis.
View SolutionFind the area enclosed between the curves
y=x2+1,y=2x−2 and the ordinates x=−1 and x = 2View SolutionThe area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is (a) 2sq.units (b) 1sq.units (c) 4sq.units (d) none of these
View SolutionFind the area enclosed between the curves
y2=2x+6 and y=x−1View SolutionFind the area enclosed between the curves
y=4x2 and y=x2+3View Solution


