The area bounded by the curves y=x(x−3)2andy=x is________ (in sq. units)
Video Solution
Text Solution
The correct Answer is:8
Required area =2∫20(x(x−3)2−x)dx=8 sq. units
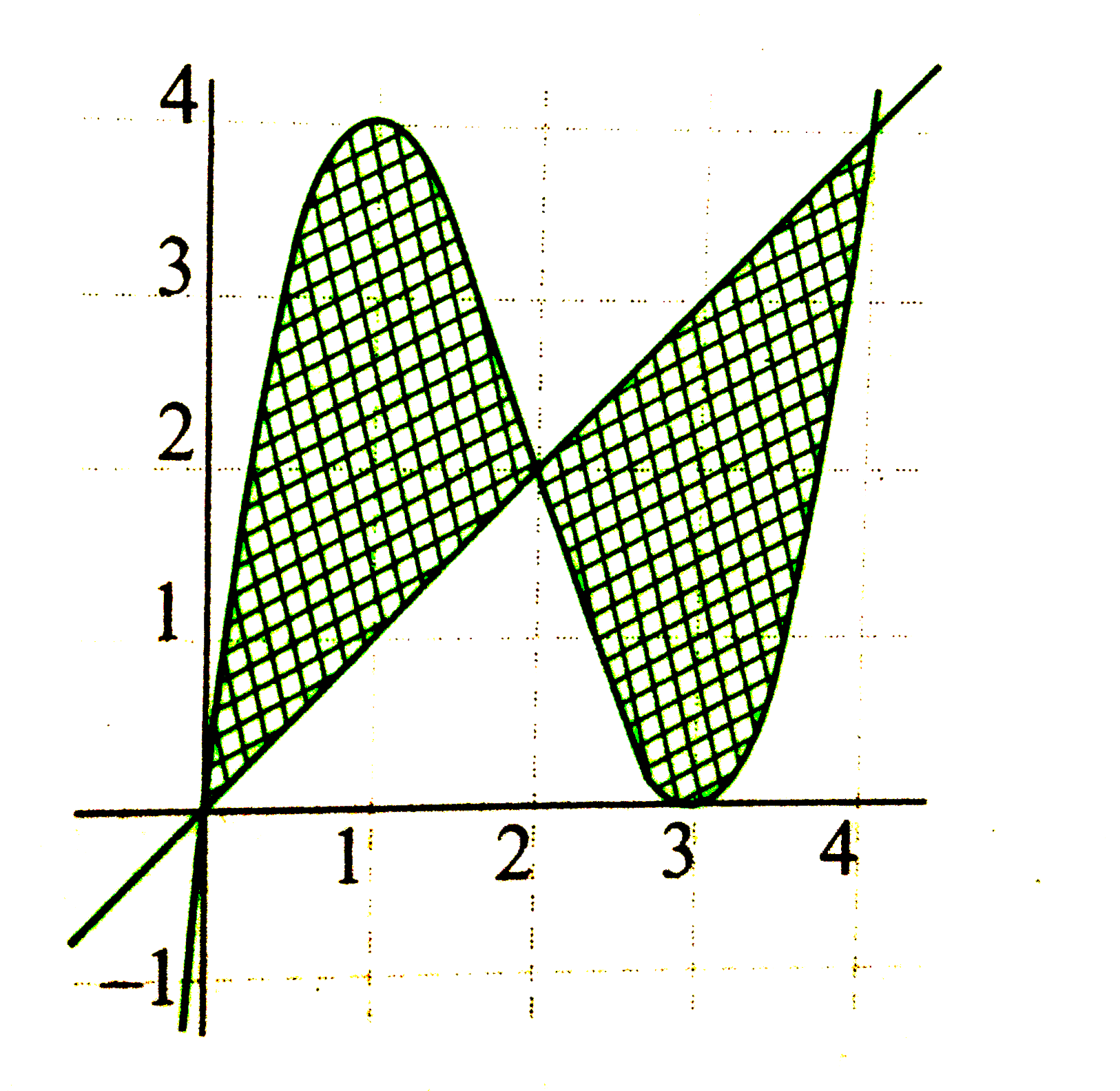
|
Topper's Solved these Questions
- AREABook:CENGAGEChapter:AREAExercise:JEE Main Previous Year
Explore 10 Videos
- AREABook:CENGAGEChapter:AREAExercise:JEE Advanced Previous Year
Explore 9 Videos
- AREABook:CENGAGEChapter:AREAExercise:Exercise (Matrix)
Explore 4 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGEChapter:APPLICATIONS OF DERIVATIVESExercise:Question Bank
Explore 29 Videos
- AREA UNDER CURVESBook:CENGAGEChapter:AREA UNDER CURVESExercise:Question Bank
Explore 20 Videos
Similar Questions
Knowledge Check
The area bounded by the curves y2=x3and|y|=2x is
A516 sq unitsB165 sq unitsC38 sq unitsDNone of these
The area bounded by the curves y=x(x−3)2andy=x is________ (in sq. units)
View SolutionThe area bounded by the curves y=2−|2−x| and |x|y=3 is
View SolutionThe area bounded by the curves y=x3−x and y=x2+x is (In sq, units)
View SolutionThe area (in sq. units) bounded by the curves y=x (x−3)2 and y=x is
View SolutionArea bounded by the curve y≥|x−2|andy≤4−|x−3|
View SolutionArea bounded by the curves y=x2−1,x+y=3 is
View SolutionThe area bounded by the curve y=3|x|andy+|2−x|=2 is
View Solution

