The area bounded by the curves y=xex,y=xe−x and the line x=1 is 2esq.units (b) 1−2esq.units 1esq.units (d) 1−1esq.units
2e sq. units
1−2e sq. units
1e sq. units
1−1e sq. units
The correct Answer is:A
Curve tracing : y=xex
Let dydx=0⇒ex+xex=0orx=−1.
Also, at x=−1,dydx changes sign from -ve to + ve,
Hence, x=-1 is a point of minima.
When x→∞,yrar∞
Also limx→−∞xex=limx→−∞xe−x=limx→−∞1e−x=0
With similar types of arguments, we can draw the graph of y=xe−x.
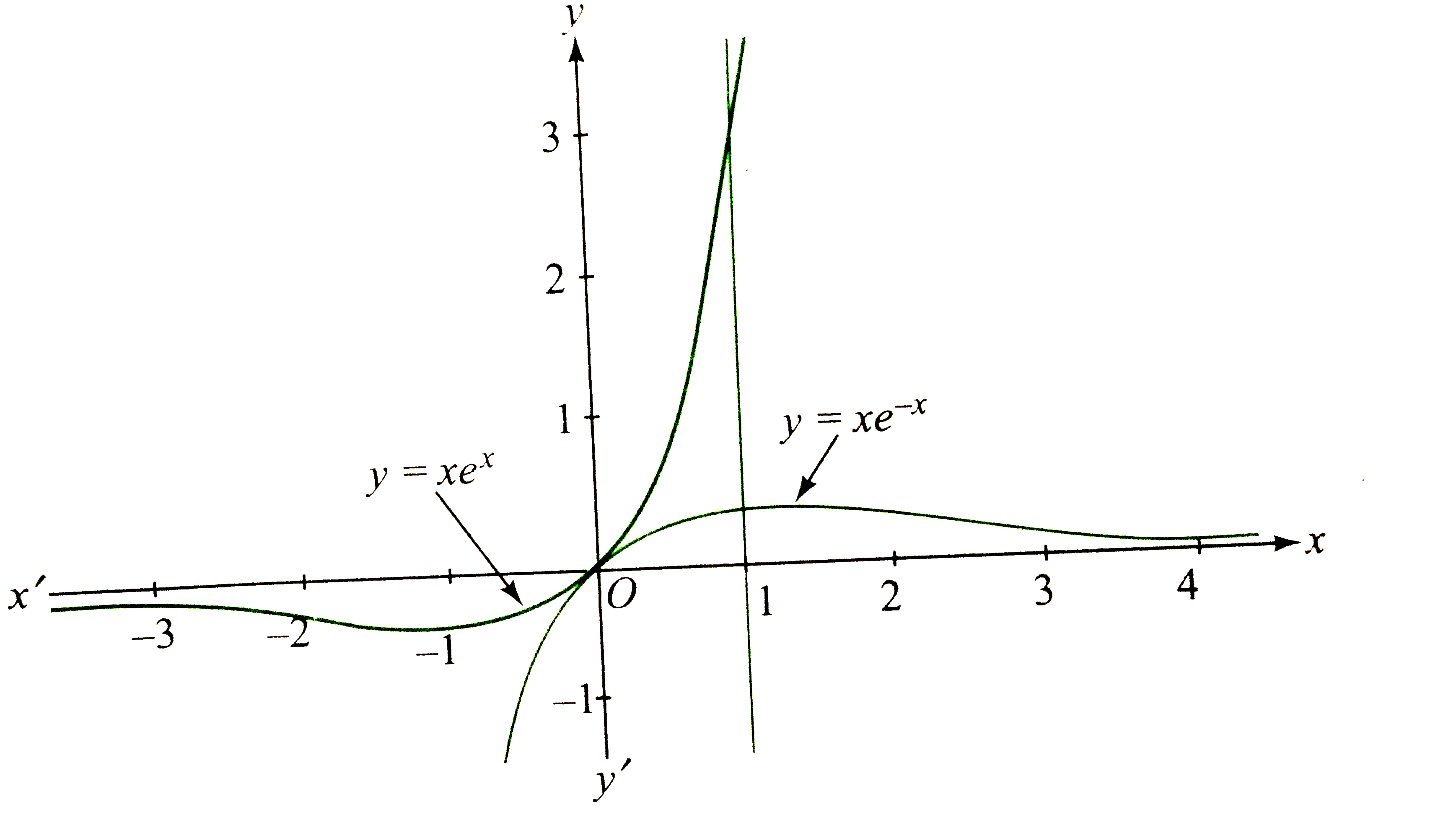
Required ara =∫10xexdx−∫10xe−xdx
=[xex]10−∫10exdx−([−xe−x]10+∫10e−xdx)
=e−(e−1)−(−e−1−(e−1−1))=2e sq. units
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Multiple Correct Answers Type13videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Linkded Comprehension Type21videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.37videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
The area bounded by the two branches of curve (y−x)2=x3 and the straight line x=1 is (a) 15sq.units (b) 35sq.units 45sq.units (d) 84sq.units
View SolutionThe area bounded by the two branches of curve (y−x)2=x3 and the straight line x=1 is 15sq.units (b) 35sq.units 45sq.units (d) 84sq.units
View SolutionA particle of mass m is moving anticlockwise, in a circle of radius R in x−y plane with centre at (R,0) with a constant speed v2. If is located at point (2R,0) at time t=0. A man starts moving with a velocity v1 along the positive y-axis from origin at t=0. Calculate the linear momentum of the particle w.r.t. man as a function of time.
View SolutionThe area bounded by the curves y=sinx between the ordinates x=0, x=π and the x-axis is 2 sq.units b. 4 sq.units c. 3 sq.units d. 1 sq.units
View SolutionThe area bounded by the curve a2y=x2(x+a) and the x-axis is a23sq.units (b) a24sq.units 3a24sq.units (d) a212sq.units
View SolutionLet f(x)=x3+3x+2andg(x) be the inverse of it. Then the area bounded by g(x) , the x-axis, and the ordinate at x=−2andx=6 is (a) 94sq.units (b) 43sq.units (c) 54sq.units (d) 73sq.units
View SolutionThe area of the region bounded by x=0,y=0,x=2,y=2,y≤ex and y≥1nx is (a) 6−41n2sq.units (b) 41n2−2sq.units 21n2−4sq.units (d) 6−21n2sq.units
View SolutionThe area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is (a) 2sq.units (b) 1sq.units (c) 4sq.units (d) none of these
View SolutionConsider two curves C1:y2=4[√y]xandC2:x2=4[√x]y, where [.] denotes the greatest integer function. Then the area of region enclosed by these two curves within the square formed by the lines x=1,y=1,x=4,y=4 is (a)83sq.units (b) 103sq.units (c)113sq.units (d) 114sq.units
View SolutionA copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is μs What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
View Solution


