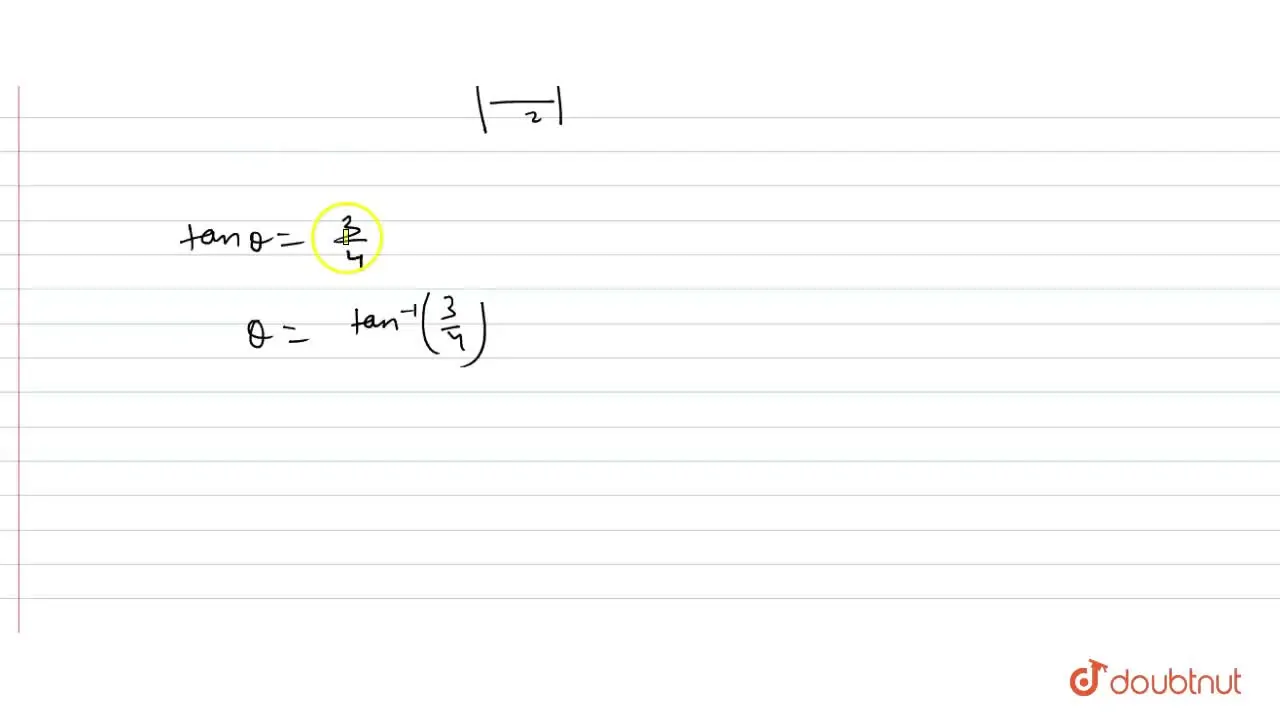The angle of intersection of the curves y=x2andx=y2 at (1,1) is
A
tan−1(43)
B
tan−1(1)
C
90∘
D
tan−1(34)
Video Solution
Text Solution
The correct Answer is:D
The slope of the curve
y=x2⇒dydx=2x
∴(dydx)11=2=m1
and slope of the curve
x=y2
⇒1=2ydydx
⇒dydx=12y⇒(dydx)11=12=m2
∴ Angle of intersection at the point (1,1) is
tanθ=m1−m21+m1m2=2−121+2×12=34
∴θ=tan−1(3)4
|
Updated on:21/07/2023
Related Playlists
Similar Questions
The angle of intersection of the curves y=x2,6y=7−x3 at (1, 1), is
View SolutionAngle of intersection of the curves y=4−x2 and y=x2 is
View SolutionFind angle of intersection of the curves y=4−x2 and y=x2.
View SolutionThe angle of intersection of the curves y=x2,6y=7−x3 at (1, 1), is
View SolutionThe angle of intersection of the curves y=x2,6y=7−x3 at (1, 1), is
View SolutionFind the angle of intersection of the curves y2=xandx2=y
View SolutionThe angle of intersection of the curves x2+y2=6 and y2=x ,is
View SolutionFind the angle of intersection of the curves y=4−x2 and y=x2
View SolutionFind the angle of intersection of the curves y=x2andy=4−x2.
View SolutionFind the angle of intersection of curves y=x3 and 6y=7−x2 at point (1,1)
View Solution