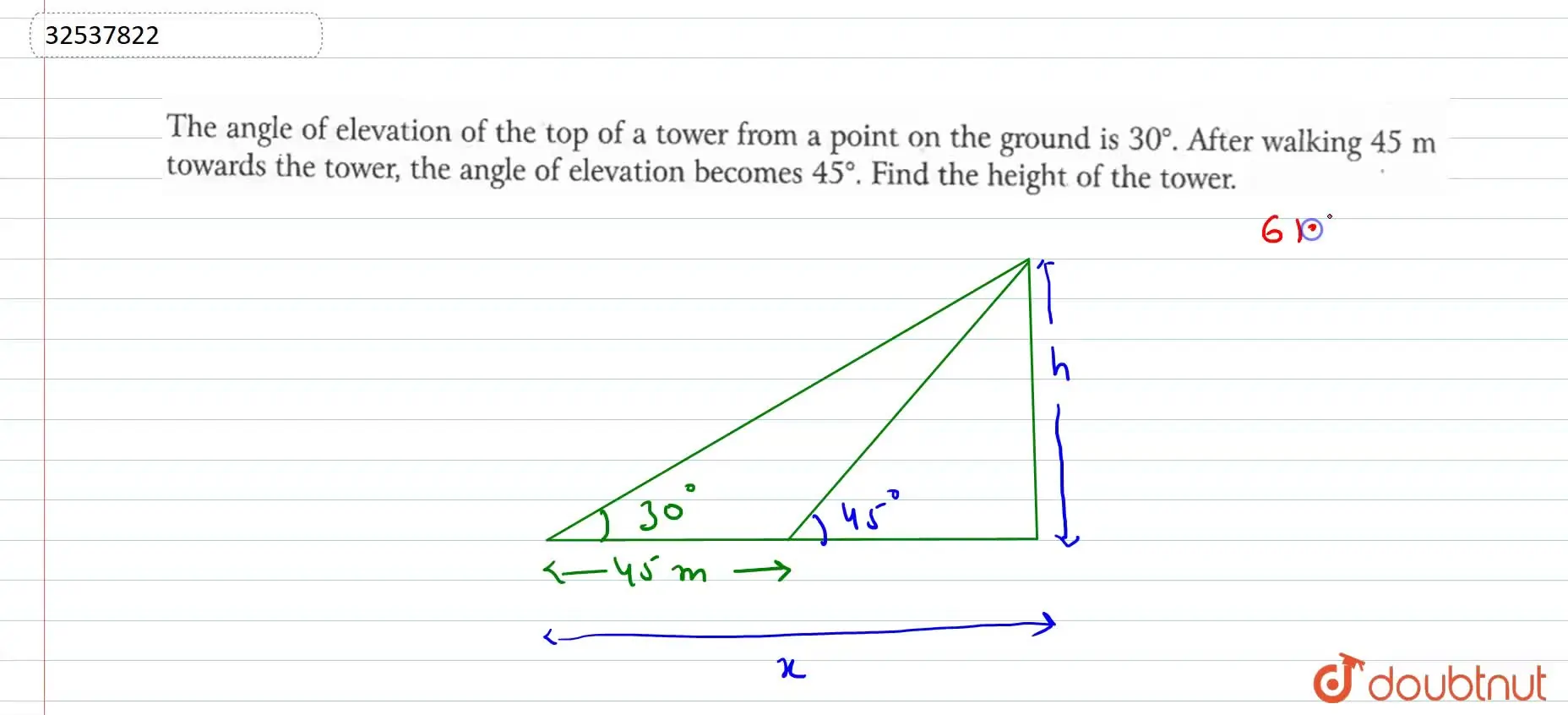
The angle of elevation of the top of a tower from a point on the ground is 30∘. After walking 45 m towards the tower, the angle of elevation becomes 45∘. Find the height of the tower.
The correct Answer is:61.47 m
Step by step video, text & image solution for The angle of elevation of the top of a tower from a point on the ground is 30^(@). After walking 45 m towards the tower, the angle of elevation becomes 45^(@). Find the height of the tower. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Revision Exercise (short Answer Questions)5videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Revision Exercise (long Answer Questions)1videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Long Answer Questions5videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - REAL NUMBERSEXERCISE - Revision Exercise Long Answer Questions5videos
REAL NUMBERS
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions5videos
STATISTICS
Similar Questions
The angle of elevation of the top of a tower from a point on the ground is 30∘. After walking 40√3 m towards the tower, the angle of elevation becomes 60∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower at point on the ground is 30∘. If on walking 20 metres towards the tower, the angle of elevation become 60∘ then the height of the tower is
View SolutionThe angle of elevation of the top of a tower at a point on the ground is 30∘. If on walking 20 m toward the tower, the angle of elevation becomes 60∘, then the height of the tower is
View SolutionThe angle of elevation of the top of a tower at a point G on the ground is 30∘. On walking 20 m towards the tower the angle of elevation becomes 60∘. The height of the tower is equal to :
View SolutionProblems of finding the height of tower if angle of elevation is changing on walking away/towards the tower.; ex-1 The angle of the elevation of the top of the tower at a point on the ground is 300. On walking 24m towards the tower the angle of elevation changes from 600. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower at a point A on the ground is 30∘. On walking 20 meters toward the tower, the angle of elevation is 60∘. Find the height of the tower and its distance from A.
View SolutionThe angle of elevation of the top of a tower at a point on the ground is 30o . On walking 24 m towards the tower, the angle of elevation becomes 60o . Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower at a point on level ground is 45∘. When moved 20 m towards the tower, the angle of elevation becomes 60∘.What is the height of the tower ?
View SolutionThe angle of elevation of the top of a tower at a point A on the ground is 30∘. On walking 20 meters toward the tower, the angle of elevation is 60∘. Find the height of the tower and its distance from A.
View SolutionThe elevation of the top of a tower from a point on the ground is 45∘ . On travelling 60 m from the point towards the tower, the alevation of the top becomes 60∘ . The height of the tower, in metres, is
View Solution