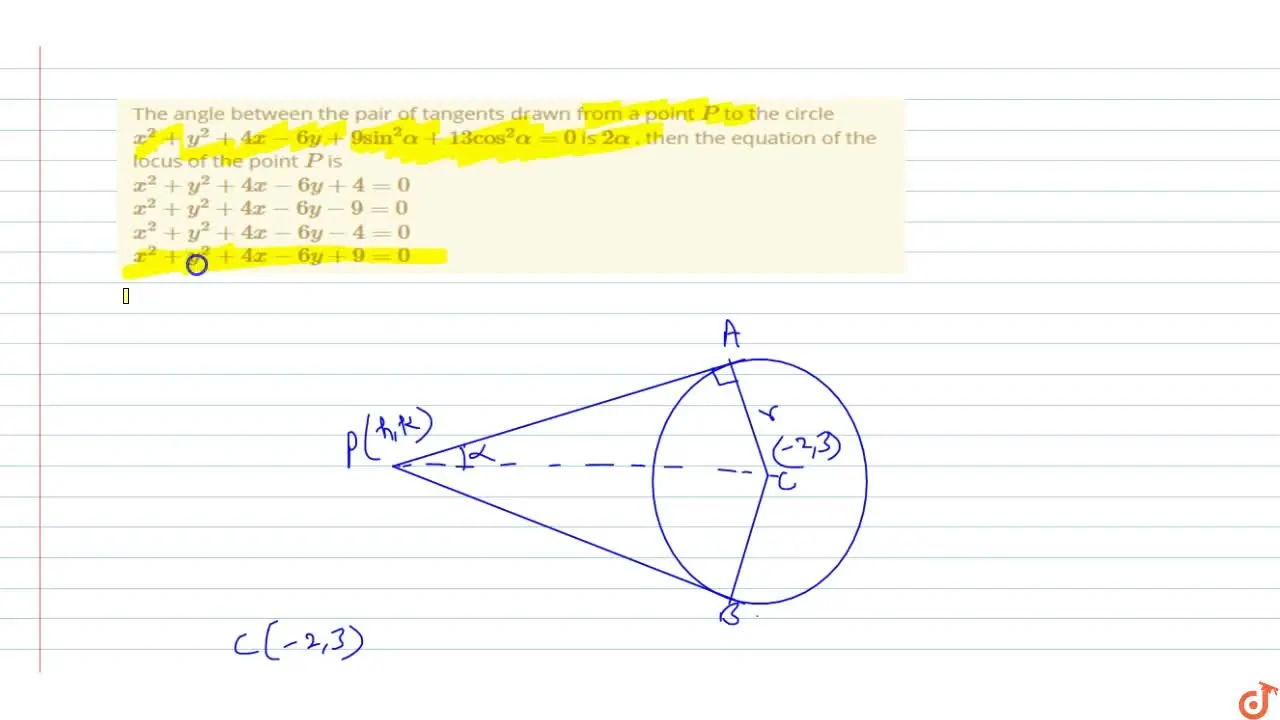
The angle between the pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α . then the equation of the locus of the point P is x2+y2+4x−6y+4=0 x2+y2+4x−6y−9=0 x2+y2+4x−6y−4=0 x2+y2+4x−6y+9=0
let the coordinates of P are(h,k)
the angle made by P to the tangents is 2α
the centre of the circle is C(−2,3)
so, r=√4+9−9sinα−13cos2α
r=√4+9cos2α−13cosα
=√4−4cos2α
=√4(sin2α)
=2sinα
in ∠APC
sinα=ACPC=2sinα√(h+2)2+(k−3)2
=√(h+2)2+(k−3)2=2
h2+k2+4k−6k+13=4
locus of P(h,k) is x2+y2+4x−6y+9=0
option D is correct
Related Playlists
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Solved Examples And Exercises439videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - JEE Previous Year (Multiple Question)11videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
Similar Questions
The angle between the pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α . then the equation of the locus of the point P is x2+y2+4x−6y+4=0 x2+y2+4x−6y−9=0 x2+y2+4x−6y−4=0 x2+y2+4x−6y+9=0
View SolutionThe angle between a pair of tangents from a point P to the circe x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α. Find the equation of the locus of the point P.
View SolutionThe angle between a pair of tangents drawn from a point T to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is . The equation of the locus of the point T is
View SolutionCombined equation to the pair of tangents drawn from the origin to the circle x2+y2+4x+6y+9=0 is
View SolutionCombined equation to the pair of tangents drawn from the origin to circle x2+y2+4x+6y+9=0 is
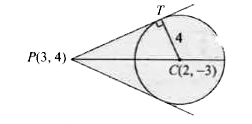
View SolutionFind the length of a tangent drawn from the point (3,4) to the circle x2+y2−4x+6y−3=0.
 View Solution
View SolutionThe length of the chord of contact of the tangents drawn from the point (−2,3) to the circle x2+y2−4x−6y+12=0 is:
View SolutionFind the equations of the tangents from the point A(3,2) to the circle x2+y2+4x+6y+8=0.
View SolutionEquation of tangents drawn from (0,0) to x2+y2−6x−6y+9=0 are
View SolutionThe equation of the normal at (1,2) to the circle x2−y2−4x−6y−12=0 is
View Solution