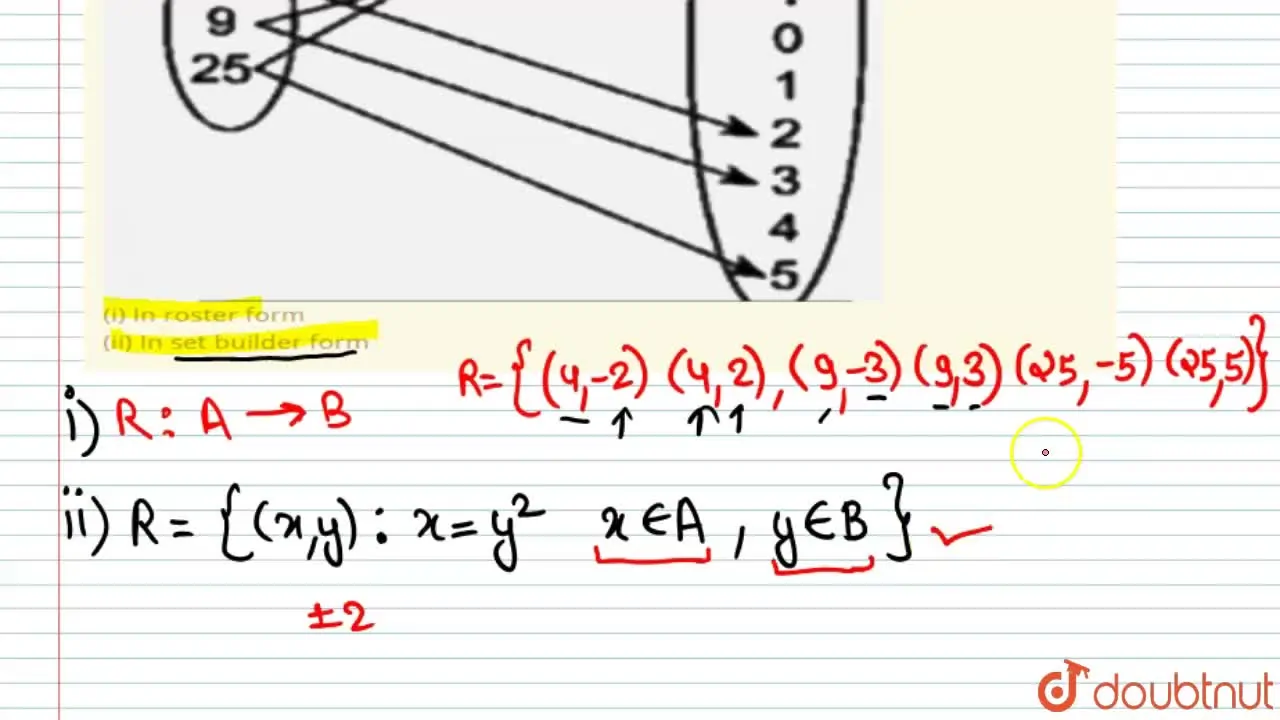
The adjoining diagram shows a relation between the set A and B. Write this relation
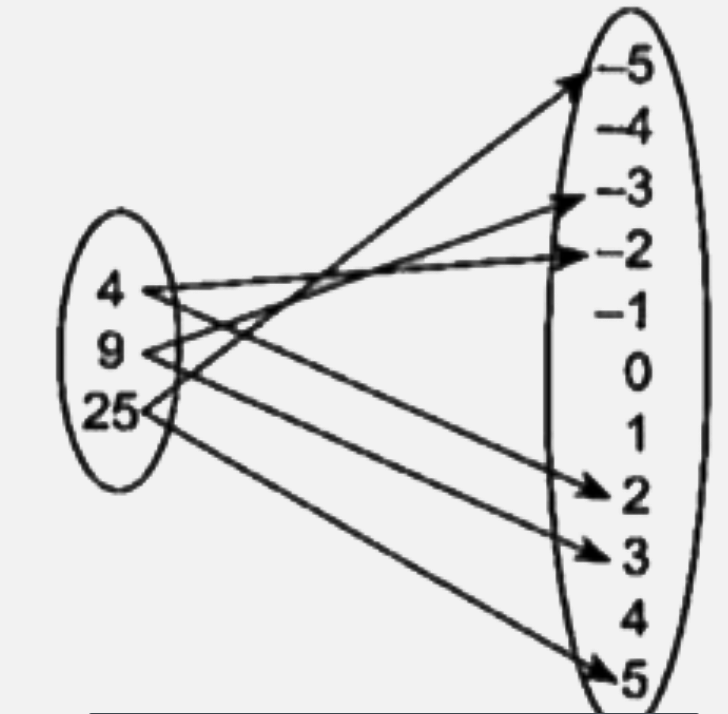
The adjoining diagram shows a relation between the set A and B. Write this relation (i) In roster form (ii) In set builder form
(i) In roster form
(ii) In set builder form

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:R={(4,2),(4,−2),(9,3),(9,−3),(25,5),(25,−5)}
(ii) R={(x,y)∣∣x=y2,ξnA,y∈B}

Updated on:21/07/2023
|
Answer

Step by step video & image solution for The adjoining diagram shows a relation between the set A and B. Write this relation (i) In roster form (ii) In set builder form by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023
Class 11MATHSMODEL TEST PAPER - 17

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The following diagram represents the solution of two sets P and Q on the number line:
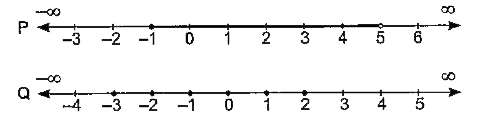
    ocr_image
    The solution set of Q in set builder form is:

    A{x:−3<x<2,x∈R}
    B{x:−3≤x≤2,x∈I}
    C{x:−3<x≤2,x∈N}
    D{x:−3≤x<2,x∈W}

  • The following diagram represents the solution of two sets P and Q on the number line:
    ocr_image
    The solution set of P in set-builder form is

    A{x:−1<x≤5,x∈R}
    B{x:−1≤x<5,x∈R}
    C{x:−1≤x≤5,x∈R}
    D{x:−1<x<5,x∈R}