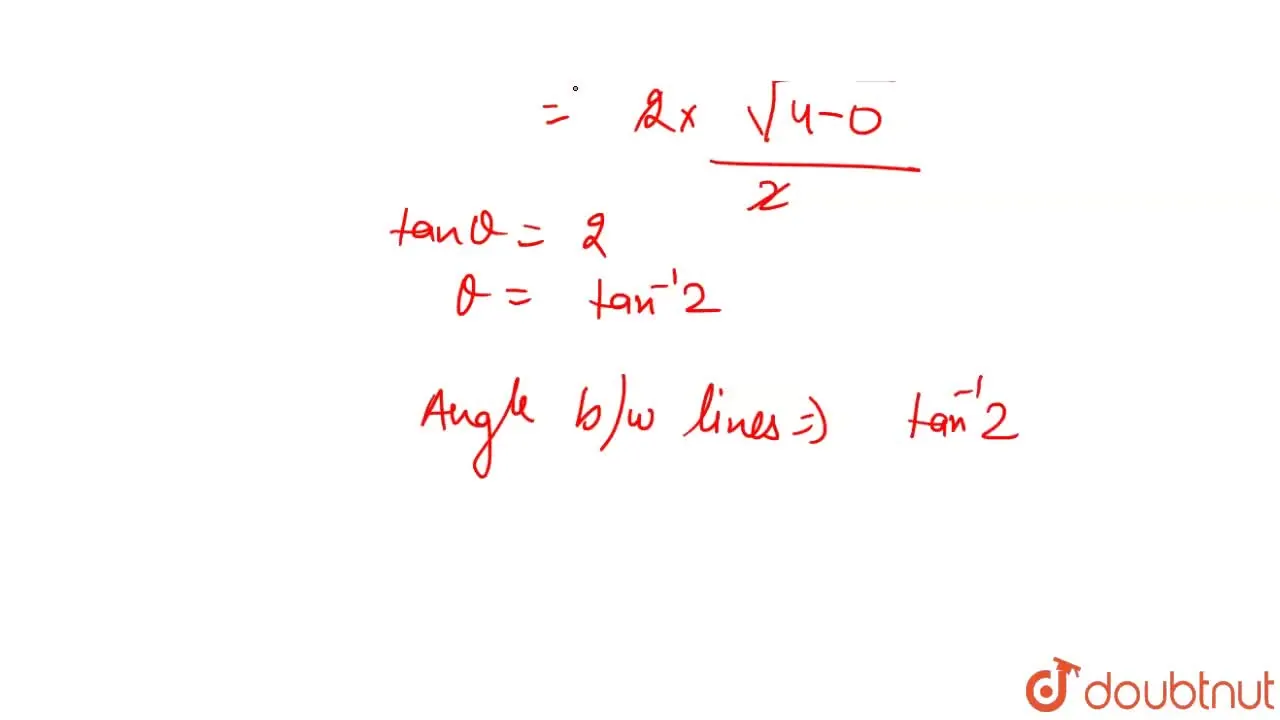The acute angle formed between the lines joining the origin to the points of intersection of the curves x2+y2−2x−1=0 and x+y=1, is
tan−1(−12)
tan−1(2)
tan−1(12)
60∘
The correct Answer is:B
Given equation , x2+y2−2x−1=0 .....(i)
and x+y=1....(ii)
Making Eq.(i) homogeneous with help of Eq.(ii) , we get x2y2−2x(x+y)−(x+y)2=0
⇒x2+y2−2x2−2xy−x2−y2−2xy=0
⇒−2x2−4xy=0
⇒2x2+4xy=0 .......(iii)
Let θ be the angle between the lines represented by Eq.(iii).
Then , tanθ=∣∣∣2√h2−aba+b∣∣∣=∣∣∣2√4−02∣∣∣
⇒tanθ=2
∴θ=tan−1(2) .
Related Playlists
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PAIR OR STRAIGHT LINES EXERCISE - MHT CET Corner13videos
PAIR OR STRAIGHT LINES
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PAIR OR STRAIGHT LINES EXERCISE - PRACTICE EXCERCISE (Excercise 1) (Topical Problems) (General Equation of Second Degree)20videos
PAIR OR STRAIGHT LINES
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MOCK TEST 5EXERCISE - MCQS50videos
MOCK TEST 5
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PLANEEXERCISE - MHT CET Corner9videos
PLANE
Similar Questions
The equation of the bisectors of the angle between the lines joining the origin to the points of intersection of the curve x2+xy+y2+x+3y+1=0 and the line x+y+2=0 is
View SolutionThe acute angle between the lines joining the origin to the points of intersection of the line √3x+y=2 and the circle x2+y2=4, is
View SolutionThe lines joining the origin to the points of intersection of 2x2+3xy−4x+1=0 and 3x+y=.1 given by
View SolutionThe equation of the line joining origin to the points of intersection of the curve x2+y2=a2 and x2+y2−ax−ay=0, is
View SolutionThe acute angle between thee lines joining the origin to the points of intersection of the line √3x+y=2 and the circle x2+y2=4, is
View SolutionThe angle between the straight lines joining the origin to the point of intersection of 3x2+5xy−3y2+2x+3y=0 and 3x−2y=1, is
View SolutionThe equation of the line joining the origin to the point of intersection of the lines 2x2+xy−y2+5x−y+2=0 is
View SolutionThe angle between the lines joining the origin to the points of intersection of the line √3x+y=2 and the curve y2−x2=4 is
View SolutionFind the angle between the straight lines joining the origin to the point of intersection of 3x2+5xy−3y2+2x+3y=0 and 3x−2y=1
View SolutionFind the values of k ,if the lines joining the origin to the points of intersection of the curve 2x2−2xy+3y2+2x−y−1=0 and the line x+2y=k are mutually perpendicular.
View Solution