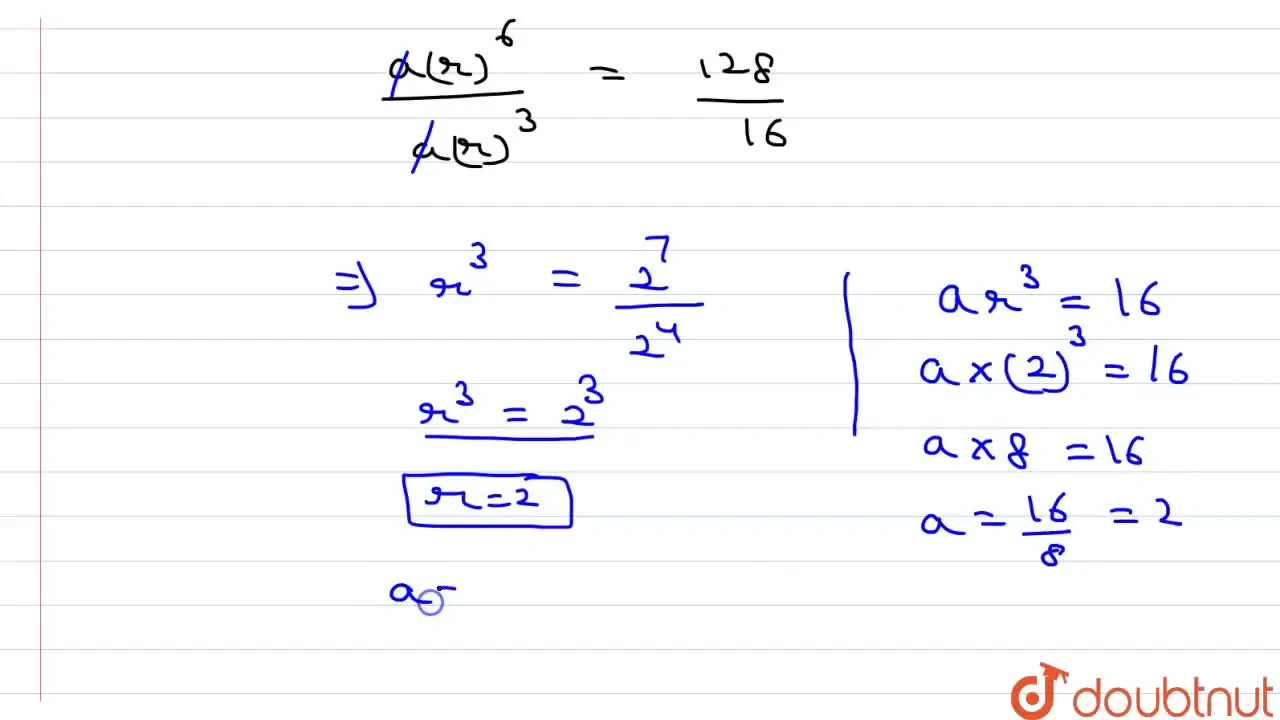The 4th term of a G.P. is 16 and 7th term is 128. Find the first term and common ration of the series.
The correct Answer is:a = 2, r = 2
Step by step video, text & image solution for The 4th term of a G.P. is 16 and 7th term is 128. Find the first term and common ration of the series. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
Similar Questions
The 5th term of an A.P. is 11 and the 9th term is 7. Find the 16th term.
View SolutionThe 4th term of an A.P. is 22 and 15th term is 66. Find the first term and the common difference. Hence, find the sum of the series to 8 terms.
View SolutionThe 11th term of an A.P. is 80 and the 16th term is 110. Find the 31st term.
View SolutionThe fourth term of a G.P. is 27 and the 7th term is 729, find the G.P.
View SolutionThe sum of 4th and 8th terms of an A.P. is 24 and the sum of the 6th and 10th terms is 34. Find the first term and the common difference of the A.P.
View SolutionThe sum of 4th and 8th terms of an A.P. is 24 and the sum of the 6th and 10th terms is 34. Find the first term and the common difference of the A.P.
View SolutionThe 7th term of a H.P. is 110 and 12 th term is 125, find the 20th term of H.P.
View SolutionIf (2p)th term of a G.P is q2 and (2q)th term is p2 then (p+q)th term is
View SolutionIf the 3rd and the 6th terms of an A.P. are 7 and 13 respectively, find the first' term and the common difference.
View SolutionThe nth term of a GP is 128 and the sum of its n terms is 255. If its common ratio is 2 then its first term is.
View Solution