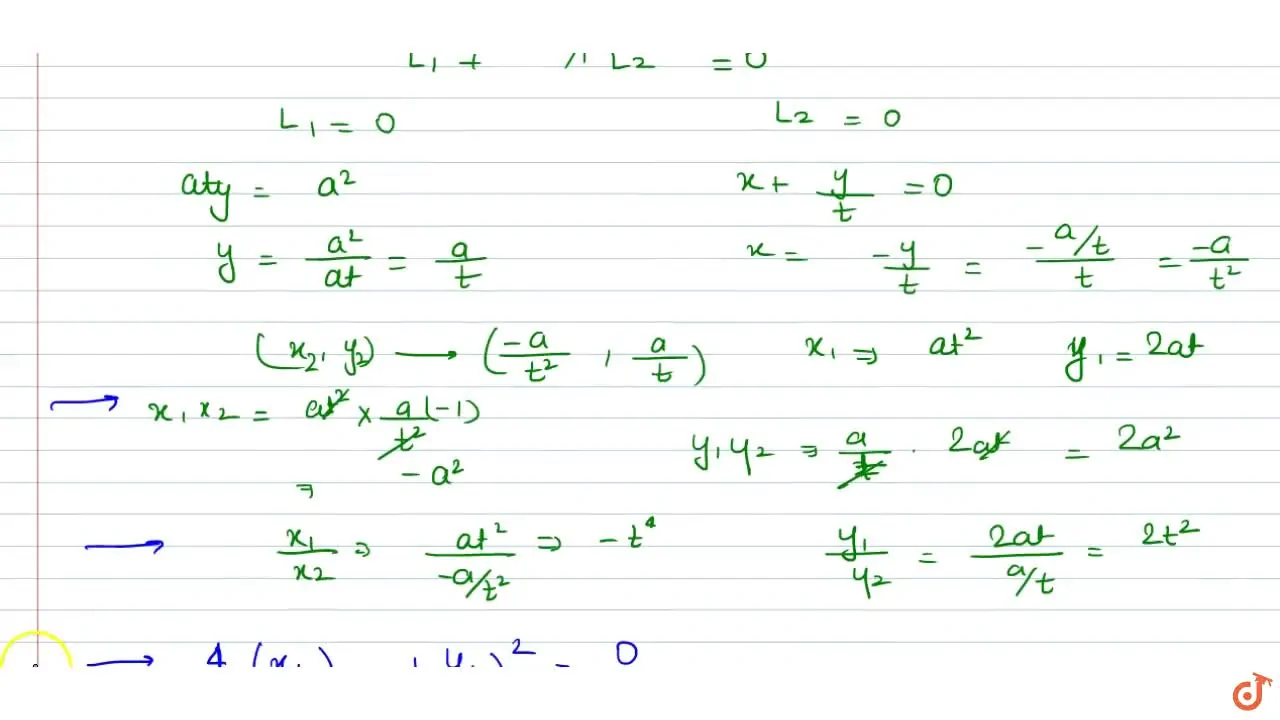Tangent is drawn at any point (x1,y1) other than the vertex on the parabola y2=4ax . If tangents are drawn from any point on this tangent to the circle x2+y2=a2 such that all the chords of contact pass through a fixed point (x2,y2), then x1a,x2 in GP (b) y12,a,y2 are in GP −4,y1y2,x1/x2 are in GP (d) x1x2+y1y2=a2
x1,a,x2 are in GP
y12,a,y2 are in GP
−4y1y2,x1x2 are in GP
x1x2+y1y2=a2
The correct Answer is:B, C, D
2,3,4
Let (x1,y1)≡(at2,2at).
Tangent at this point is ty=x+at2.
Any point on this tangent is ((h,(h+at2)/t).
The chord of contact of this point with respect to the circle
x2+y2=a2 is
hx+h+at2ty=a2
or(aty−a2)+h(x+yt)=0
which is a family of straight lines passing through the point of intersection of
ty−a=0andx+yt=0
So, the fixed point is (−a/t2,a/t). Therefore,
x2=−at2,y2=at
Clearly, x1x2=−a2,y1y2=2a2
Also, x1x2=−t4
and y1y2=2t2
or4x1x2+(y1y2)2=0
Related Playlists
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Comprehension)41videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Matrix)4videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Single)98videos
PARABOLA
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank19videos
PERMUTATION AND COMBINATION
Similar Questions
Tangent is drawn at any point (x1,y1) other than the vertex on the parabola y2=4ax . If tangents are drawn from any point on this tangent to the circle x2+y2=a2 such that all the chords of contact pass through a fixed point (x2,y2), then (a)x1,a,x2 in GP (b) y12,a,y2 are in GP (c)−4,y1y2,(x_1//x_2)are∈GP(d)x_1x_2+y_1y_2=a^2
View SolutionTangent is drawn at any point (x1,y1) on the parabola y2=4ax . Now tangents are drawn from any point on this tangent to the circle x2+y2=a2 such that all the chords of contact pass throught a fixed point (x2,y2) Prove that 4(x1x2)+(y1y2)2=0.
View SolutionA tangent is drawn at any point (l,m)l,m≠0 on the parabola y2=4ax and the tangents are drawn from any point on this tangent to the circle x2+y2=a2 (where a>0) such that all chords of contact pass through a fixed point (α,β), then
View Solutiontangent is drawn at point P(x1,y1) on the hyperbola x24−y2=1. If pair of tangents are drawn from any point on this tangent to the circle x2+y2=16 such that chords of contact are concurrent at the point (x2,y2) then
View SolutionIf the tangents are drawn from any point on the line x+y=3 to the circle x2+y2+9, then the chord of contact always passes through fixed point. Find that point
View SolutionFrom, a point on line y=x+k ,tangents are drawn to x22−y21=1such that chords of contact pass through a fixed point (a,b) then ab=
View SolutionFrom every point on the line x+y=4 ,tangents are drawn to circle x2+y2=4 .Then,all chord of contact passes through (x1,y1),x1+y1=
View SolutionTangents are drawn from any point on the ellipse x29+y24=1 to the circle x2+y2=1 and respective chord of contact always touches a conic 'C', then -
View SolutionThe equation of tangents drawn from the point (0,1) to the circle x2+y2−4x−2y+4=0 are
View SolutionTangents are drawn to x2+y2=1 from any arbitrary point P on the line 2x+y−4=0.Prove that corresponding chords of contact pass through a fixed point and find that point.
View Solution