Sum the following geometric series to infinity:
(a)(√2+1)+1+(√2−1).............+∞
(b)12+133+123+134+125+136..........+∞
Video Solution
Text Solution
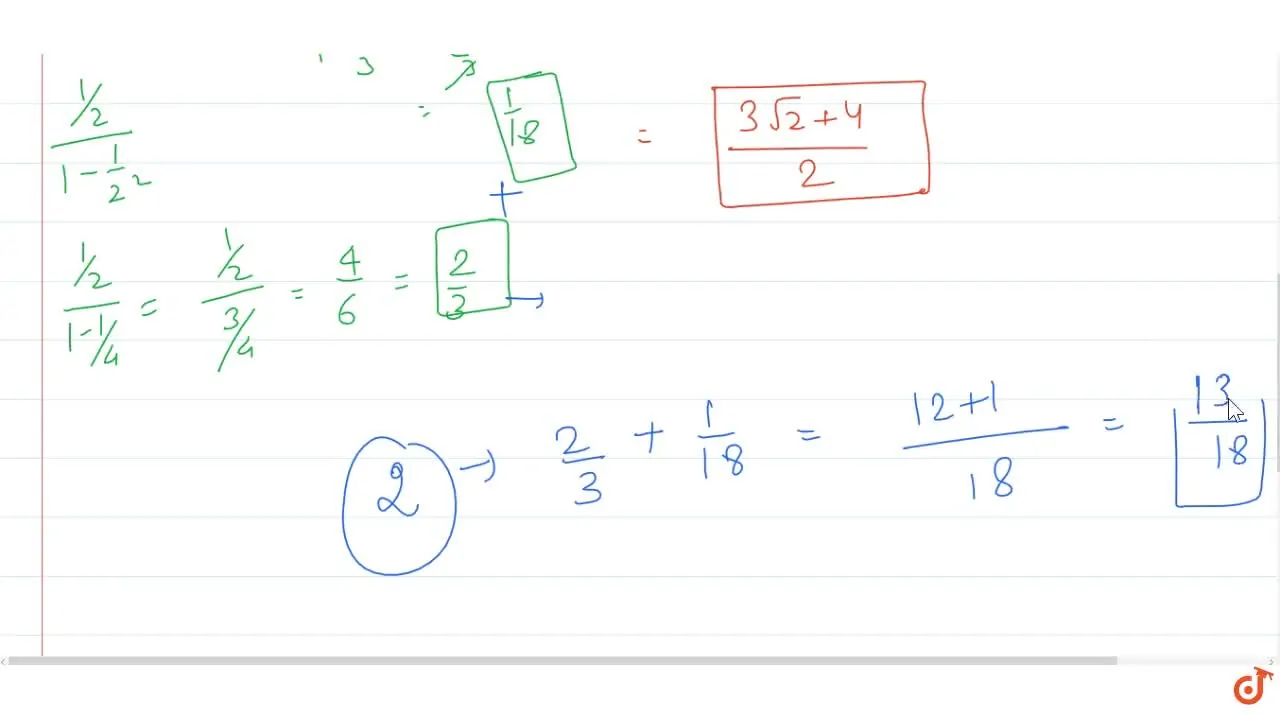
(i)Given,
(√2+1)+1+(√2−1).............+∞
r=(√2−1) and a=(√2+1)
sum of infinite series is a1−r
⇒√2+11−(√2−1)
⇒√2+12−√2
⇒√2+12−√2×2+√22+√2
⇒4+3√24−2
⇒4+3√22
(ii) 12+133+123+134+125+136+....∞
⇒(12+123+125+....∞)+(133+134+135+....∞)
⇒121−122+1331−(13)
⇒124−14+1333−13
⇒(42)×(14−1)+(333)×(13−1)
⇒23+118
⇒1318
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Sum the following geometric series to infinity:
(a)(√2+1)+1+(√2−1).............+∞
(b)12+133+123+134+125+136..........+∞View SolutionFind the sum of the following series: (√2+1)+1+(√2−1)+.......+∞
View SolutionFind the sum of the following series to infinity: 1−13+132−133+134+∞
View SolutionIf S=11.2−12.3+13.4−14.5+...∞
View SolutionFind the sum of the following geometric series:2/9-1/3+1/2-3/4+ to 5 terms.
View SolutionFind the sum of the following series to infinity: 13+152+133+154+135+156+∞
View Solution11.2+1.31.2.3.4+1.3.51.2.3.4.5.6+.....∞
View SolutionFind the sum to infinity of the series: 1+32+522+723+..........∞
View SolutionThe sum of 12+13.(123)+15.(125)+....∞ is
View SolutionFind the sum of each of the following infinite series :
√2−1√2+12√2−14√2+...∞View Solution