Derive mirror formula for a convex mirror.Solution in Punjabi
New Cartesian sign conventions :
(i) All the distances are measured from the pole of the mirror.
(ii) All the distances measured in the direction of incident ray are taken as positive and those opposite to the direction of incident ray are taken as negative.
(iii) All distances measured in vertically upward direction from the principal axis are taken as positive and in vertically downward direction as negative.
Mirror formula A relation between distance of object, distance of image from mirror and focal length of the mirror is known as mirror formula.
Derivation of mirror formula : Let an object AB is held perpendicular to principal axis of concave mirror beyond C and it forms the real and inverted image A.B between C and F as shown in Fig:
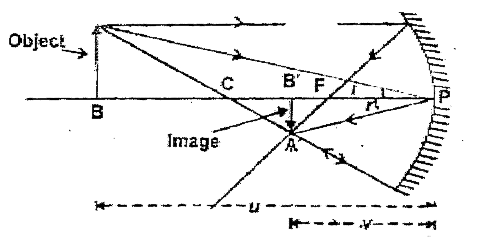
As triangles ABC and A.BC axe similar,
....(1)
Again triangles ABPand A.BP are similar,
.....(2)
From eqns. (1) and (2), we have
..(3)
Measuring all distances from P, we have
From eq. (3),
Using new Cartesian sign conventions, we have PB = -U (Distance of object measured against incident light) PC= - R"(Radius of curvature measured against incident light) PB =-v (Distance of. image measured against incident light) We get from eqn. (4)
We get from eqn. (4)
or
Cross multiplying
or ...(5)
Dividing both sides by uvR, we get
But we know that R = 2f
which is the required mirror formula.
Related Playlists
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - REFLECTION OF LIGHT EXERCISE - MOST EXPECTED QUESTIONS (1 Mark)3videos
REFLECTION OF LIGHT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - REFLECTION OF LIGHT EXERCISE - MOST EXPECTED QUESTIONS (2 Marks)4videos
REFLECTION OF LIGHT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - REFLECTION OF LIGHT EXERCISE - SHORT ANSWER TYPE QUESTIONS (3 Marks)1videos
REFLECTION OF LIGHT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - RADIOACTIVITY EXERCISE - MOST EXPECTED QUESTIONS6videos
RADIOACTIVITY
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - NUMERICAL PROBLEMS36videos
REFRACTION OF LIGHT
Similar Questions
What is the minimum size of the plane mirror , in which a man can see his full height?Explain.
02:02View SolutionDifferentiate between a real image and a virtual image.
17:06View SolutionWhen an object is placed beyond centre of curvature of a concave mirror, the image is formed:
05:31View SolutionWhat are γ-rays?
07:01View SolutionA convex lens of refractive index 1.5 has a focal length of 18 cm in air.Calculate the change in focal length,when it is immersed in water of refractive index 4/3.
11:57View SolutionUsing mirror formula, explain why does a convex mirror always produce a virtual image.
54:22View SolutionObtain an expression for mirror formula (either for concave or convex mirror).
View Solutionदर्पण सूत्र का उपयोग यह व्युत्पन्न करने के लिए कीजिए कि उत्तल दर्पण द्वारा सदैव आभासी प्रतिबिम्ब बनता है जो बिम्ब की स्थिति पर निर्भर नहीं करता।
View Solutionदर्पण सूत्र का उपयोग यह व्युत्पन्न करने के लिए कीजिए कि उत्तल दर्पण द्वारा सदैव आकार में छोटा प्रतिबिम्ब, दर्पण के ध्रुव व फोकस के बीच बनता है।
04:57View Solutionकिसी उत्तल दर्पण के लिए दर्पण समीकरण व्युतपन्न कीजिए ।
01:01:35View SolutionImage Formation By Convex Mirror | Mirror Formula | Magnification
07:58View SolutionDerive mirror equation for a convex mirror. Usingit, show that a convex mirror always produces a virtual image, independent of the location of object.
10:24View SolutionWith the help of a suitable ray diagram, derive the mirror formula for a concave mirror.
10:24View Solution(a) With the help of a suitable ray diagram, derive the mirror formula for a concave mirror.
02:43View SolutionConcave & Convex Mirror||Focal Length||Mirror Formula
View SolutionDerive mirror formula for concave mirror stating assumptions?
05:12View Solution


