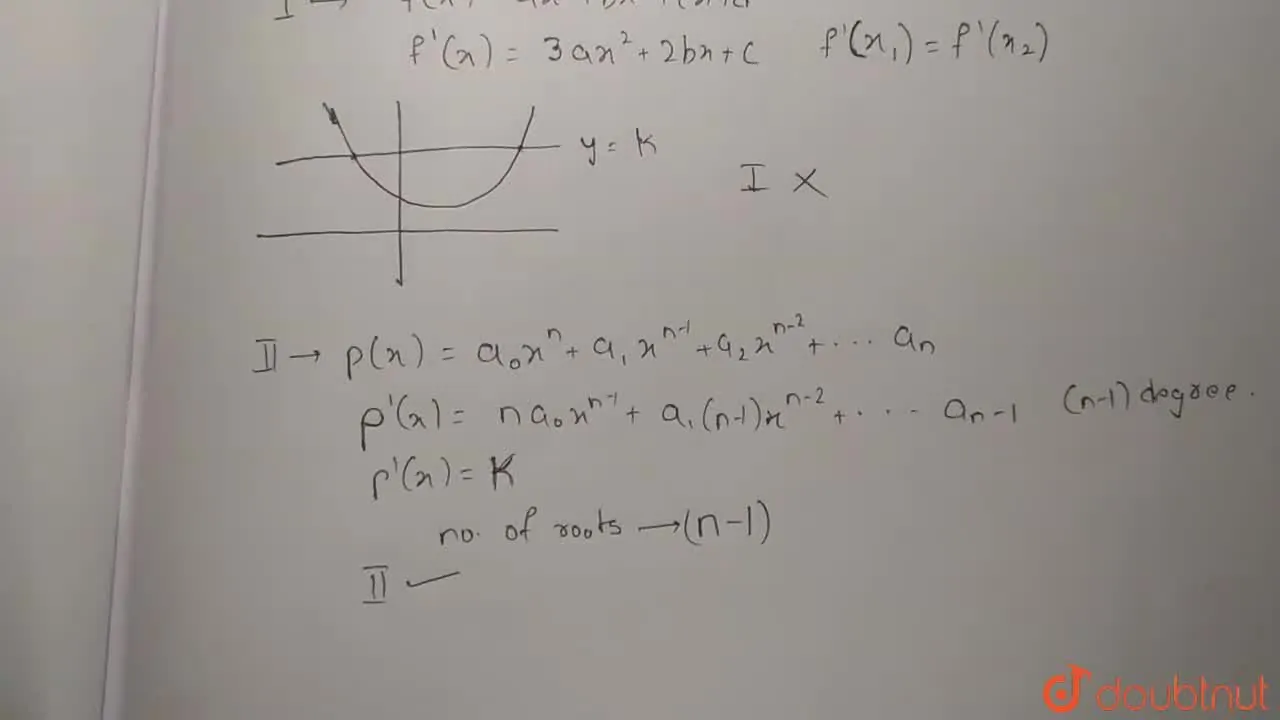Statements I Tangents at two distinct points of a cubic polynomial cannot coincide.
Statement II If p(x) is a polynomial of degree n(n≥2), then p'(x)+k cannot hold for n or more distinct values of x.
Statement I is true, Statement II is also true, Statement II is the correct explanation of Statement I.
Statement I is true, Statement II is also true, Statement II is not the correct explanation of Statement I
Statement I is true, Statement II is false
Statement I is false, Statement II is true
The correct Answer is:D
Step by step video, text & image solution for Statements I Tangents at two distinct points of a cubic polynomial cannot coincide. Statement II If p(x) is a polynomial of degree n(nge2), then p'(x)+k cannot hold for n or more distinct values of x. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ARIHANT MATHSCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Passage Based Questions)8videos
DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS
- BOOK - ARIHANT MATHSCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Matching Type Questions)1videos
DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS
- BOOK - ARIHANT MATHSCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (More Than One Correct Option Type Questions)15videos
DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS
- BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 104videos
DIFFERENTIATION
- BOOK - ARIHANT MATHSCHAPTER - ELLIPSEEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)27videos
ELLIPSE
Similar Questions
p(x)=√2 is a polynomial of degree
View SolutionIf P (x) is polynomial of degree 2 and P(3)=0,P'(0)=1,P''(2)=2, then p(x)=
View SolutionLet P (x) and Q (x) be two polynomials of degree 5, then degree of P (x) + Q (x) si
View SolutionIf p(x) is a n degree polynomial the number of roots are
View SolutionIf ∫(tan9x)dx=f(x)+log|cosx|, where f(x) is a polynomial of degree n in tan x, then the value of n is
View SolutionLet P(x) be a polynomial of degree 11 such that P(x)=1x+1 for x=0,1,2,3,….11. The value of P(12) is.
View SolutionIf a is defined by f (x)=a0xn+a1xn−2+a2xn−2+...+an−1x+an where n is a non negative integer and a0,a1,a2,…….,an are real numbers and a0≠0, then f is called a polynomial function of degree n. For polynomials we can define the following theorem
(i) Remainder theorem: Let p(x) be any polynomial of degree greater than or equal to one and 'a' be a real number. if p(x) is divided by (x-a), then the remainder is equal to p(a).
(ii) Factor theorem : Let p(x) be a polynomial of degree greater than or equal to 1 and 'a' be a real number such that p(a) = 0, then (x-a) is a factor of p(x). Conversely, if (x-a) is a factor of p(x). then p(a)=0.
The factor of the polynomial x3+3x2+4x+12 isView SolutionIf a is defined by f (x)=a0xn+a1xn−2+a2xn−2+...+an−1x+an where n is a non negative integer and a0,a1,a2,…….,an are real numbers and a0≠0, then f is called a polynomial function of degree n. For polynomials we can define the following theorem
(i) Remainder theorem: Let p(x) be any polynomial of degree greater than or equal to one and 'a' be a real number. if p(x) is divided by (x-a), then the remainder is equal to p(a).
(ii) Factor theorem : Let p(x) be a polynomial of degree greater than or equal to 1 and 'a' be a real number such that p(a) = 0, then (x-a) is a factor of p(x). Conversely, if (x-a) is a factor of p(x). then p(a)=0.
THe polynomials P(x)=kx3+3x2−3andQ(x)=2x3−5x+k, when divided by (x−4) leave the same remainder. Then the value of k isView SolutionLet P(x) be a polynomial of degree 11 such that P(x)=1x+1, for x=0,1,2,...11. The value of P(12) is
View SolutionIf a is defined by f (x)=a0xn+a1xn−2+a2xn−2+...+an−1x+an where n is a non negative integer and a0,a1,a2,…….,an are real numbers and a0≠0, then f is called a polynomial function of degree n. For polynomials we can define the following theorem
(i) Remainder theorem: Let p(x) be any polynomial of degree greater than or equal to one and 'a' be a real number. if p(x) is divided by (x-a), then the remainder is equal to p(a).
(ii) Factor theorem : Let p(x) be a polynomial of degree greater than or equal to 1 and 'a' be a real number such that p(a) = 0, then (x-a) is a factor of p(x). Conversely, if (x-a) is a factor of p(x). then p(a)=0.
The remainder when the polynomial P(x)=x4−3x2+2x+1 is divided by x−1 isView Solution