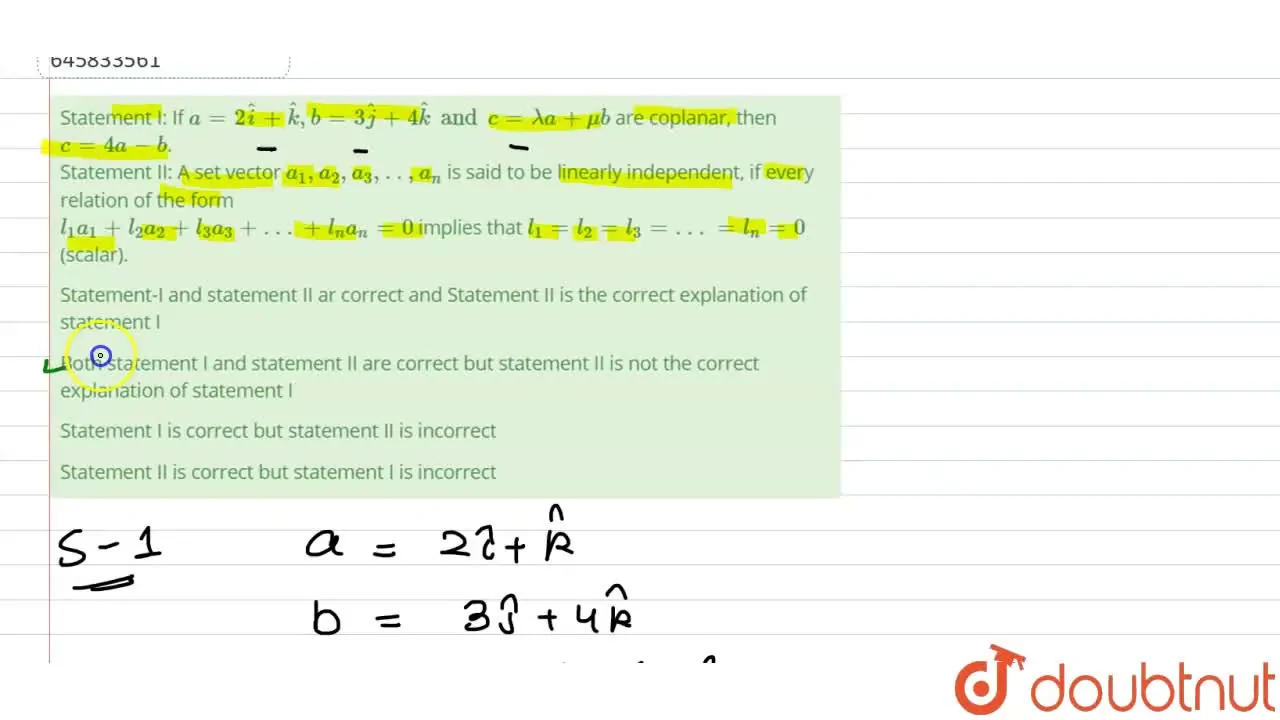
Statement I: If a=2ˆi+ˆk,b=3ˆj+4ˆkandc=λa+μb are coplanar, then c=4a−b.
Statement II: A set vector a1,a2,a3,..,an is said to be linearly independent, if every relation of the form
l1a1+l2a2+l3a3+...+lnan=0 implies that l1=l2=l3=...=ln=0 (scalar).Solution in Gujrati
Statement-I and statement II ar correct and Statement II is the correct explanation of statement I
Both statement I and statement II are correct but statement II is not the correct explanation of statement I
Statement I is correct but statement II is incorrect
Statement II is correct but statement I is incorrect
The correct Answer is:B
a,b and c are coplanar c=λa+μb⇒λ=4andμ=−1.
Similar Questions
If a_(1),a_(2) , a_(3),"……..",a_(n) are in H.P. , then : (a_(1))/( a_(2) + a_(3) +"........."+a_(n)),(a_(2))/(a_(1) + a_(3)+"..........."+a_(n)),"......",(a_(n))/(a_(1)+a_(2)+"........"a_(n-1)) are in :
05:25View SolutionIf a1,a2,a3,…….,an are in A.P. and a1=0, then the value of (a3a2+a4a3+....+anan−1)−a2(1a2+1a3+....+1an−2) is equal to
05:51View SolutionLines x=n,y=n3 intersect at the point An.Ln is a line through An parallel to x+y=0 and make an intercept of length ln on the axis of x, then the value of 5∑n=1ln is equal to K4−16, where K =
04:05View SolutionLet L1 and L2 be two lines intersecting at P. If A1,B1,C1 are points on L1,A2,B2,C2,D2,E2 are points on L2 and if none of these coincides with P, then the number of triangles formed by these 8 points is
04:37View SolutionIf a1,a2,a3,... are in A.P. and ai>0 for each i, then n∑i=1na23i+1+a13i+1a13i+a23i is equal to (a) na2/3n+a1/3n+a2/31 (b) n(n+1)a2/3n+a1/3n+a2/31 (c) n(n−1)a2/3n+a1/3n⋅a1/31+a2/31 (d) None of these
06:36View Solutionagreed L_(1) :_(1)x + b_(1)y + c_(1)=0, L_(2):a_(2)x + b_(2)y + c_(2)=0 And L_(3):a_(3)x + b_(3)y +c_(3)=0 is. Statement - I: L_(1) : L_(2) : L_(3) If there are three congruent lines, |{:(a_(1),b_(1),c_(1)),(a_(2),b_(2),c_(2)),(a_(3),b_(3),c_(3)):}|=0 Will happen. Because Statement-II: If |{:(a_(1),b_(1),c_(1)),(a_(2),b_(2),c_(2)),(a_(3),b_(3),c_(3)):}|=0 If you have lines L_(1),L_(2) And L_(3) Will be concurrent.
03:48View SolutionIf a1,a2,a3,…., an are the terms of arithmatic progression then prove that 1a1a2+1a2a3+1a3a4+….+1an−1an=n−1a1an
04:00View SolutionIf a1,a2,a3,a4,,……,an−1,an are distinct non-zero real numbers such that (a21+a22+a23+…..+a2n−1)x2+2(a1a2+a2a3+a3a4+……+an−1an)x+(a22+a23+a24+......+a2n)≤0 then a1,a2,a3,.....,an−1,an are in
03:11View Solution