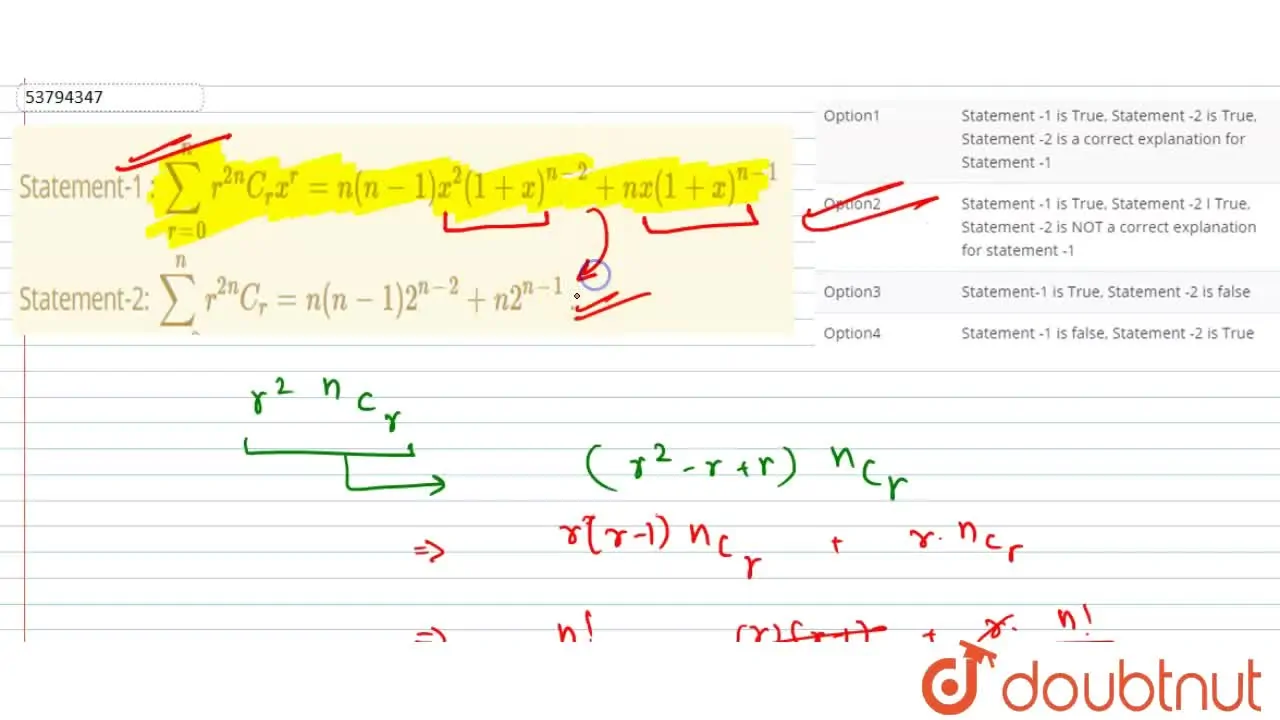
Statement-1 : n∑r=0r2nCrxr=n(n−1)x2(1+x)n−2+nx(1+x)n−1
Statement-2: n∑r=0r2nCr=n(n−1)2n−2+n2n−1 .
A
1
B
2
C
3
D
4
Video Solution
Text Solution
The correct Answer is:b
We have,
n∑r=0r2nCrxr
=n∑r=0{r(r−1)+r}nCrxr
=n∑r=0r(r−1)nCrxrn∑r=0rnCrxr
n∑r=0r(r−1)×nr×n−1r−1n−2Cr−2xr−2x2+n∑r=1r×nr×n−1Cr−1xr−1×x
=n(n−1)x2n∑r=2n−1Cr−2xr−2+nxn∑r=1n−1Cr−1xr−1
=n(n−1)x2(1+x)n−2+nx(1+x)n−1
So, statement-2 s also true.
Clearly, statement-1 is a correct expanation for statememt -2.
But, statement-2 is not a correct expanation for statement-1.
|
Updated on:21/07/2023
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Exercise107videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Chapter Test60videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Section I - Solved Mcqs100videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Exercise29videos
CARTESIAN CO-ORDINATE SYSTEM
Similar Questions
n∑r=1r.2nCr=
View SolutionStatement-1: n∑r=01r+1nCr=1(n+1)x{(1+x)n+1−1}−1
Statement-2: n∑r=0nCrr+1=2n+1n+1.View SolutionStatement-1 n∑r=0rnCrxr(−1)r=nx(1−x)n−1
Statement-2:n∑r=0rnCrxr(−1)r=0View SolutionEvaluate : n∑r=1nCr2r
View SolutionStatement -1: n∑r=0r(nCr)2=n(2n−1Cn−1)
Statement-2: n∑r=0(nCr)2=2nCnView SolutionStatement-1: n∑r=0(r+1)nCr=(n+2)2n−1
Statement -2: n∑r=0(r+1)nCrxr=(1+x)n+nx(1+x)n−1View SolutionStatement -2: n∑r=0(−1)rnCrr+1=1n+1
Statement-2: n∑r=0(−1)rnCrr+1xr=1(n+1)x{1−(1−x)n+1}View SolutionStetemet - 1: n∑r=0r.nCr=n2n−1
Statement-2: n∑r=0r.nCrxr=n(1+x)n−1xView SolutionProve that 2n∑r=0r.(2nCr)2=2.4n−1C2n−1.
View Solutionn∑r=0(−1)r nCr1+rx1+nx equals
View Solution