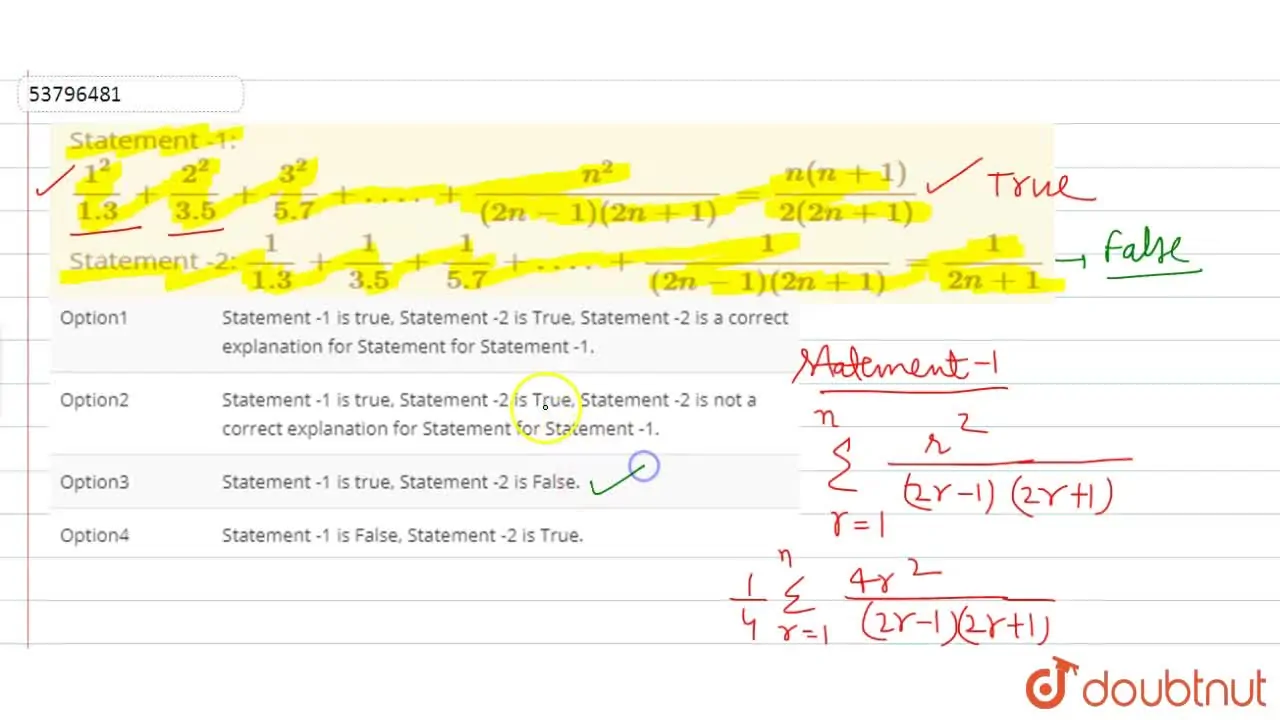
Statement -1: 121.3+223.5+325.7+....+n2(2n−1)(2n+1)=n(n+1)2(2n+1) Statement -2: 11.3+13.5+15.7+....+1(2n−1)(2n+1)=12n+1
Statement -1 is true, Statement -2 is True, Statement -2 is a correct explanation for Statement for Statement -1.
Statement -1 is true, Statement -2 is True, Statement -2 is not a correct explanation for Statement for Statement -1.
Statement -1 is true, Statement -2 is False.
Statement -1 is False, Statement -2 is True.
The correct Answer is:C
We, have
121.3+223.7+325.7+.............+n2(2n−1)(2n+1)
=n∑r=1r2(2r−1)(2r+1)
=14n∑r=14r2(2r−1)(2r+1)
=14n∑r=1(2r−1)(2r+1)+1(2r−1)(2r+1)
=14n∑r=1{1+1(2r−1)(2r+1)}
=14n∑r=11+18n∑r=1(12r−1−12r+1)
=n4+18(1−12n+1)=n(n+1)2(2n+1)
So, statement -1 is true.
Statement -2 is fals, because
11.3+13.5+15.7+.....+1(2n−1)(2n+1)
=n∑r=11(2r−1)(2r+1)=12n∑r=1(12r−1−12r+1)
=12(1−12n+1)=n2n+1
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise129videos
SEQUENCES AND SERIES
- BOOK - OBJECTIVE RD SHARMACHAPTER - SEQUENCES AND SERIESEXERCISE - Chapter Test60videos
SEQUENCES AND SERIES
- BOOK - OBJECTIVE RD SHARMACHAPTER - SEQUENCES AND SERIESEXERCISE - Section I - Solved Mcqs80videos
SEQUENCES AND SERIES
- BOOK - OBJECTIVE RD SHARMACHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Chapter Test50videos
QUADRATIC EXPRESSIONS AND EQUATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - SETSEXERCISE - Chapter Test30videos
SETS
Similar Questions
limn→∞{11.3+13.5+15.7+.....+1(2n+1)(2n+3) is equal to
View SolutionFind the sum 141×3+243×5+345×7+......+n4(2n−1)(2n+1)
View Solution141.3+243.5+345.7+......+n4(2n−1)(2n+1)=n(4n2+6n+5)48+n16(2n+1)
View Solutionlimn→∞(11.3+13.5+................+1(2n−1)(2n+1))
View Solution12+32+52+.......+(2n−1)2
=n(2n−1)(2n+1)3View Solution(2n+1)!(2n−1)!⋅(n−1)!(n+2)!=35
View Solutionlimn→∞[1n+1+1n+2+1n+3+…+12n]=
View SolutionC02+C13+C24+C35+.......+Cnn+2=1+n⋅2n+1(n+1)(n+2)
View Solution1.3+3.5+5.7+......+(2n−1)(2n+1)=n(4n2+6n−1)3
View Solution13+23+...+n31+3+5+...+(2n−1)=(n+1)24
View Solution