Question

Solve graphically the system of linear equations
$4x-5y+16=0\text{and}2x+y-6=0$.
Determine the vertices of the vertices of the triangle formed by these lines and the x-axis.

Explanation

On a graph paper, draw horizontl line `X'OX ` and vertical line `YOY'` as the x - axis and the y - axis respectively.
Graph of ` 4x - 5y + 16 = 0 `
` 4 x - 5y + 16 = 0 rArr 5y= 4x + 16`
` " "rArr y = (( 4x + 16))/( 5)" "` ... (i)
Putting ` x = - 4 ` in (i), we get `y = 0 `
Putting ` x = 1 ` in (i), we get `y = 4`
Putting ` x = 6` in (i), we get `y = 8`
Thus, we have the following table for ` 4x - 5y + 16 = 0`

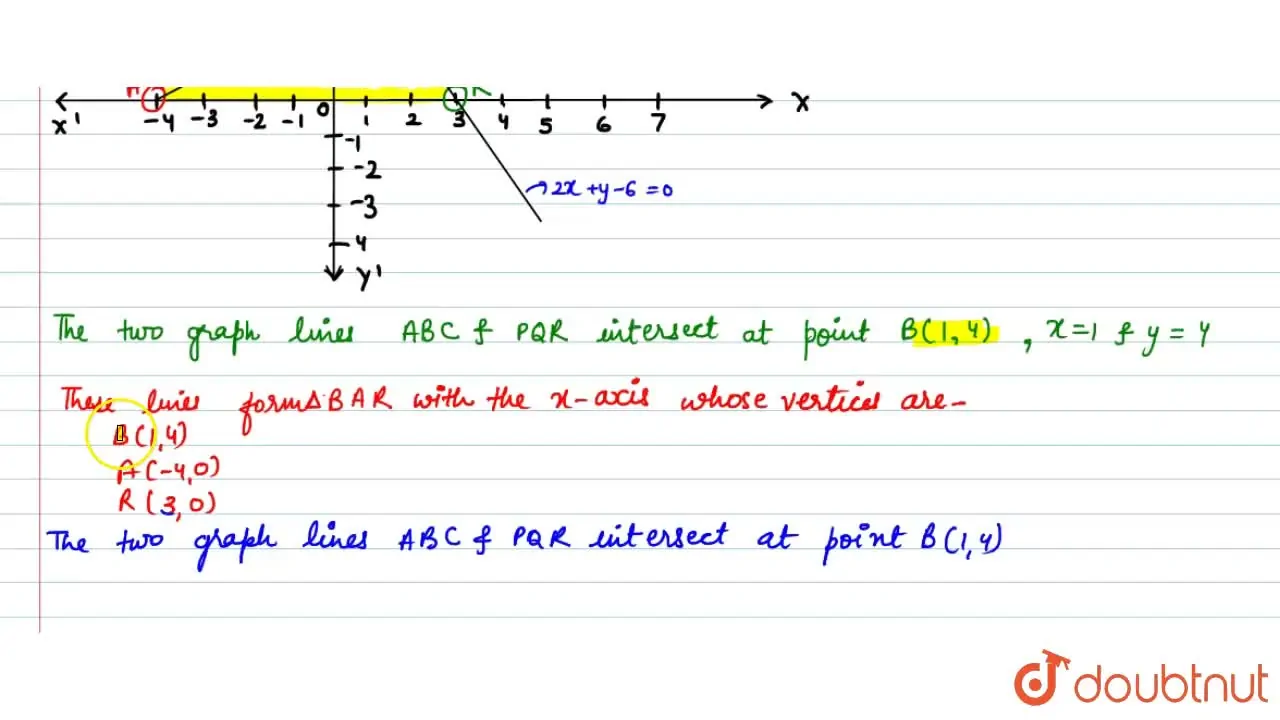
Now, plot the points ` A(-4, 0), B(1, 4)and C(6, 8)` on the graph paper.
Join AB and BC to get the graph line ABC. Extend it on both ways.
Thus, the line ABC is the graph of ` 4x - 5y + 16 = 0`
Graph of ` 2x + y - 6 = 0`
` 2x + y - 6 = 0 rArr y = ( 6 - 2x )" "`... (ii)
Putting ` x = 0 ` in (ii), we get ` y = 6 `.
Putting ` x = 2 `in (ii), we get ` y = 2 `
Putting ` x = 3 `in (ii), we get `y = 0 `
Thus, we have the following table for ` 2x + y - 6 = 0`

On the same graph paper as above, plot the points
`P(0, 6), Q(2, 2 ) and R(3, 0)`
Join PQ and QR to get the graph line PQR. Extend it on both ways.
Thus, the line PQR is the graph of ` 2x + y - 6 = 0`

The two graphs lines ABC and PQR intesect at the point ` B (1, 4 )`.
` therefore x= 1 and y = 4 ` is the solution of the given system of equations.
These lines from `Delta BAR` with the x -axis , whose vertices are ` B(1, 4), A(-4, 0) and R(3, 0)`