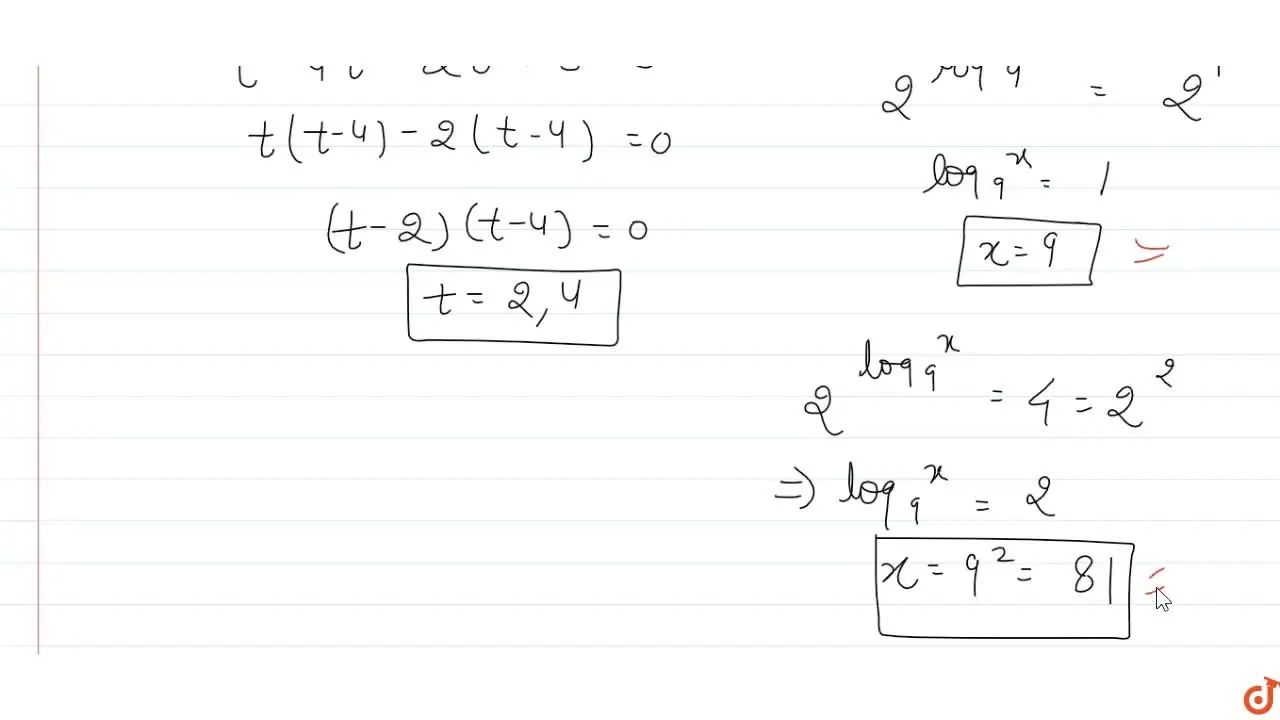Solve 4(log)9x−6x(log)92+2(log)327=0
Video Solution
Text Solution
4log9x−6xlog92+2log327=0
⇒4log9x−6⋅2log9x+2log323=0
Let 2log9x=t,
Then,
⇒t2−6t+8=0
⇒t2−4t−2t+8=0
⇒(t−4)(t−2)=0
⇒t=2ort=4
⇒2log9x=2or2log9x=4
⇒log9x=1orlog9x=2
⇒x=9orx=81.
So, value of x can be 9 or 81.
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Solve 4(log)9x−6x(log)92+2(log)327=0
View SolutionSolve 4log9x−6xlog92+2log327=0.
View SolutionThe number of solutions set of the equation 4log9x−6.xlog92+2log327=0 is
View SolutionSolve : 2(log)3x−4(log)x27≤5 (x>1)
View Solutionlogx(9x2).log23(x)=4
View SolutionSolve for x:(lg)4(log)3(log)2x=0
View Solution1log32+2log94−3log278=0
View SolutionSolve (log)48+(log)4(x+3)−(log)4(x−1)=2.
View SolutionSolve: (log)(2x+3)(6x2+23x+21)+(log)(3x+7)(4x2+12x+9)=4
View SolutionSolve(log3x)(log59)−logx25+log32=log354.
View Solution