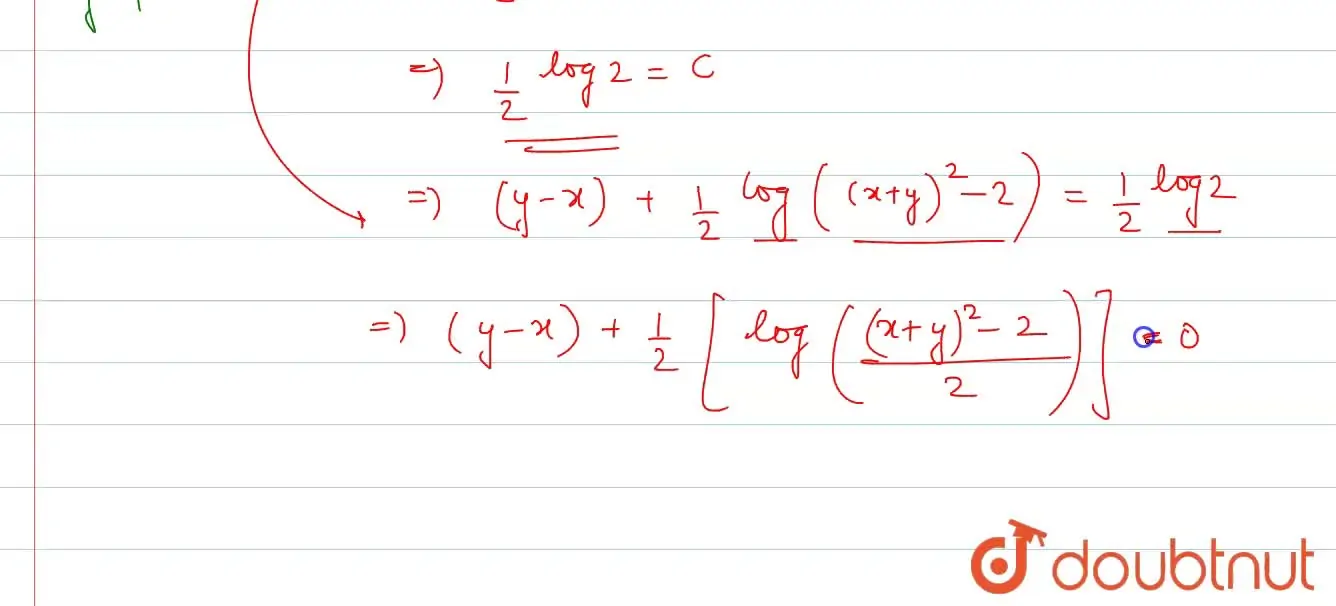Solution of the differential equation (x+y−1x+y−2)dydx=(x+y+1x+y+1), given that y=1 when x=1, is
log∣∣ ∣∣(x−y)2−22∣∣ ∣∣=2(x+y)
log∣∣ ∣∣(x−y)2+22∣∣ ∣∣=2(x−y)
log∣∣ ∣∣(x−y)2+22∣∣ ∣∣=2(x−y)
none of these
The correct Answer is:D
Let x+y=u, Then, 1+dydx=dudx
So, the given differential equation becomes
(u−1u−2)(dudx−1)=u+1u+2
⇒ dudx−1=(u+1u+2)(u−2u−1)
⇒ dudx=u2−u−2u2+u−2+1
⇒ dudx=2u2−4u2+u−2
⇒ u2+u−2u2−2du=2dx
⇒ (1+uu2−2)du=2dx
On integrating, we get
u+12log∣∣u2−2∣∣=2x+C
⇒ (x+y)+12log∣∣(x+y)2−2∣∣=2x+C
⇒ 2(y−x)+log∣∣(x+y)2−2∣∣=2C ...(i)
When x = 1, we have y = 1
∴ log2=2C
Substituting the value of C in (i), we get
2(y−x)+log∣∣(x+y)2−2∣∣=log2.
⇒ 2(y−x)+log∣∣
∣∣(x+y)2−22∣∣
∣∣=0
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Section I - Solved Mcqs48videos
DIFFERENTIAL EQUATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Section II - Assertion Reason Type5videos
DIFFERENTIAL EQUATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise26videos
DERIVATIVE AS A RATE MEASURER
- BOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIALS, ERRORS AND APPROXIMATIONSEXERCISE - Exercise17videos
DIFFERENTIALS, ERRORS AND APPROXIMATIONS
Similar Questions
Solution of the differentiable equation (x+y−1x+y−2)dydx=(x+y+1x+y+2) when y=1, is
View SolutionSolution of the differential equation x+y−1x+y−2dydx=x+y+1x+y+2,x=1,y=1, is
View SolutionSolution of the differential equation (x−y)(1−dydx)=ex is
View SolutionSolution of the differential equation dydx+1xy=3x is
View SolutionSolution of the differential equation (1+x)ydx+(1−y)xdy=0 is
View SolutionSolution of the differential equation dydx=y(1+x)x(y−1) is
View SolutionFind the particular solution of the differential equation xydydx=(x+2)(y+2), it being given that y = -1 when x = 1.
View SolutionThe solution of the differential equation 2dydx−yx=y2x2 ,given that y=2 when x=1 is
View SolutionSolution of the differential equation (1+exy)dx+exy(1−xy)dy=0 is
View SolutionSolution of the differential equation dydx=x+y+1x+y−1,y=13,x=23, is
View Solution