Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC~ΔPQR.
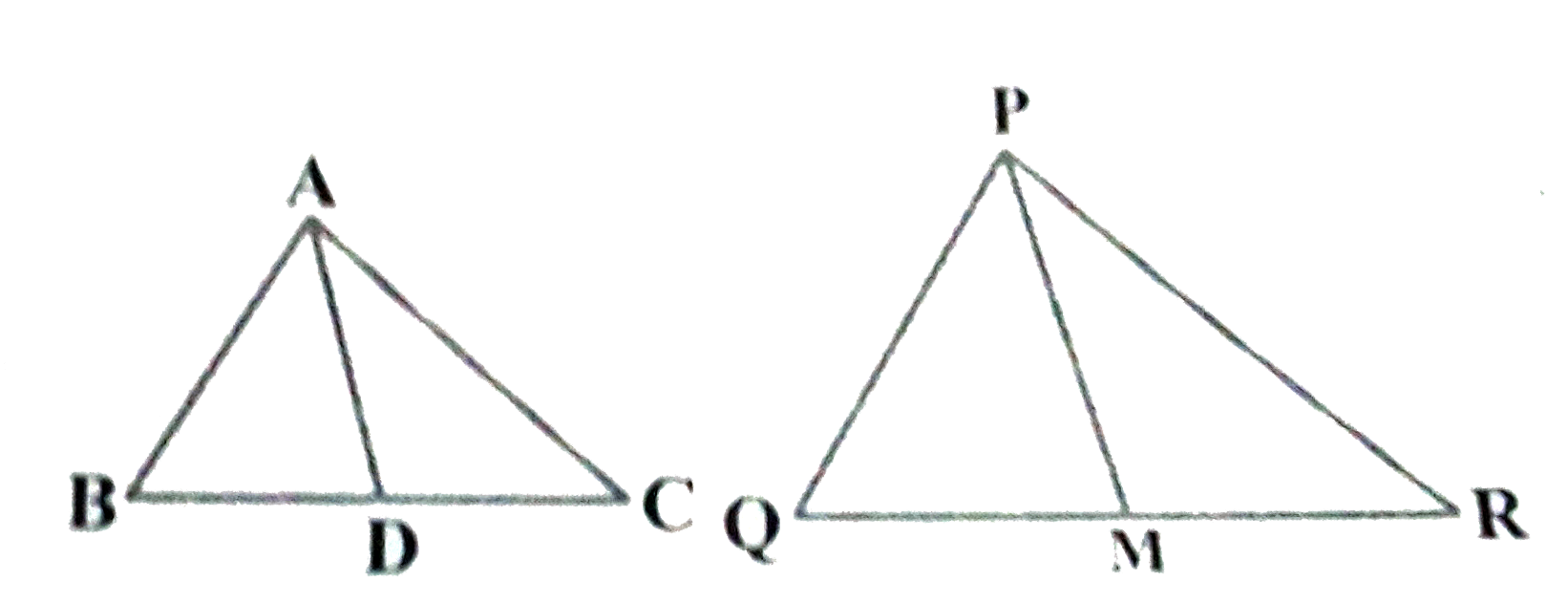
In ΔABC and ΔPQR
ABPQ=BCQR=ADPM[given]
AD and PM are median of ΔABC and ΔPQR respectively
⇒BDQM=BC2QR2=BCQR
Now, in ΔABD and ΔPQM
ABPQ=BDQM=ADPM
⇒ΔABD∼ΔPQM [SSS criterion]
Now, in ΔABC and ΔPQR
ABPQ=BCQR [given in the statement]
∠ABC = ∠PQR [∵ ΔABD ∼ ΔPQM]
⇒ ΔABC ∼ ΔPQR [SAS criterion]
Topper's Solved these Questions
- TRIANGLESBook:NCERT ENGLISHChapter:TRIANGLESExercise:Exercise 6.2
Explore 10 Videos
- TRIANGLESBook:NCERT ENGLISHChapter:TRIANGLESExercise:SOLVED EXAMPLES
Explore 14 Videos
- TRIANGLESBook:NCERT ENGLISHChapter:TRIANGLESExercise:Exercise 6.5
Explore 17 Videos
- SURFACE AREAS AND VOLUMESBook:NCERT ENGLISHChapter:SURFACE AREAS AND VOLUMESExercise:Exercise 13.3
Explore 9 Videos
Similar Questions
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC~ΔPQR.
View SolutionTwo sides AB and BC and median AD of triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR. Show that:
ΔABD=ΔPQN
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
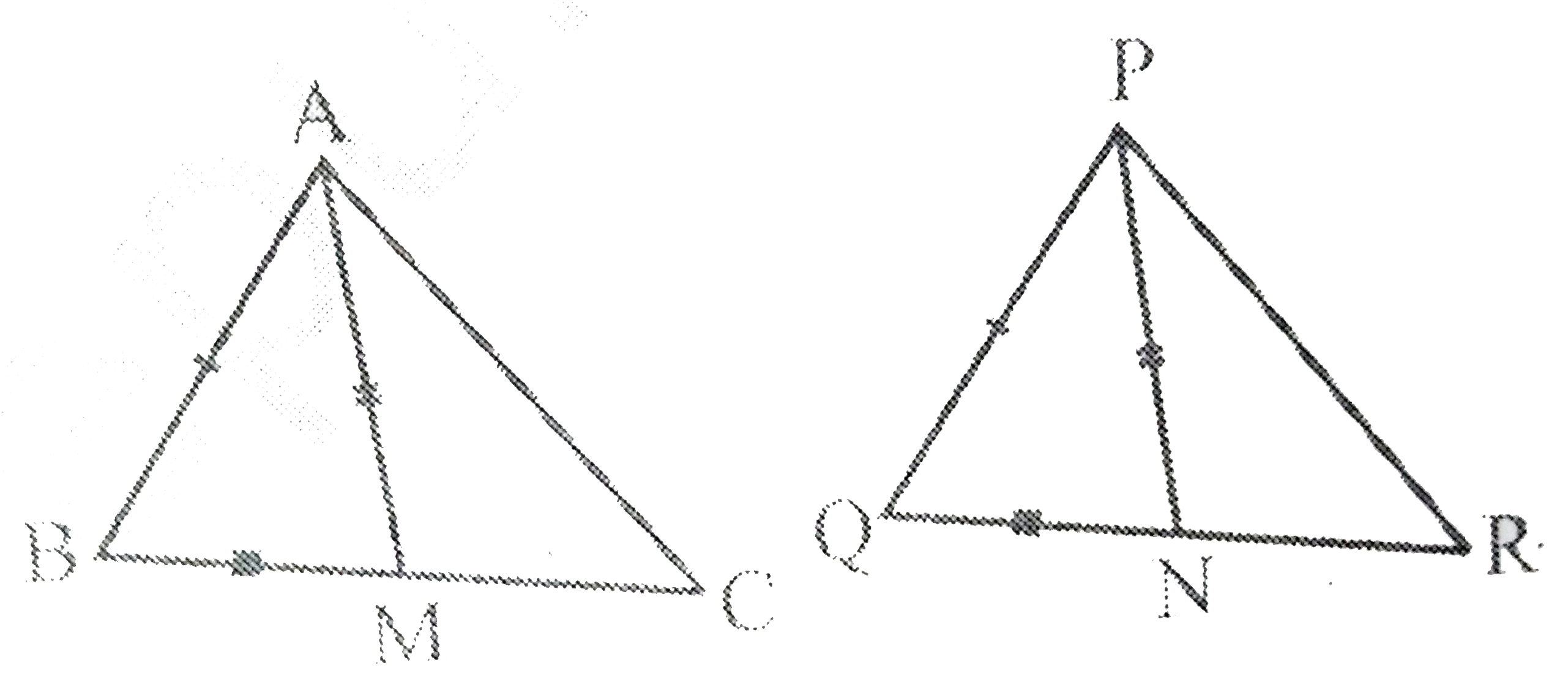
View SolutionIn the following figures, the sides AB and BC and the median AD of triangle ABC are respectively equal to the sides PQ and QR and median PS of the triangle PQR. Prove that ΔABCandΔPQR are congruent.

View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
View SolutionIn Figure, two sides AB and BC and the median AD of ABC are equal respectively to the two sides PQ and QR and the median PM of the other triangle PQR. Prove that ABD≅PQM (ii) ABC ≅ PQR
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionIf two sides and a median bisecting the third side of a triangle ar respectively proportional to the corresponding sides and median of the other triangle; then the two triangles are similar.
View SolutionIn figure, if PQ||RS, prove that ΔPOQΔSOR.
View SolutionIn Fig.9.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE).
View Solution

