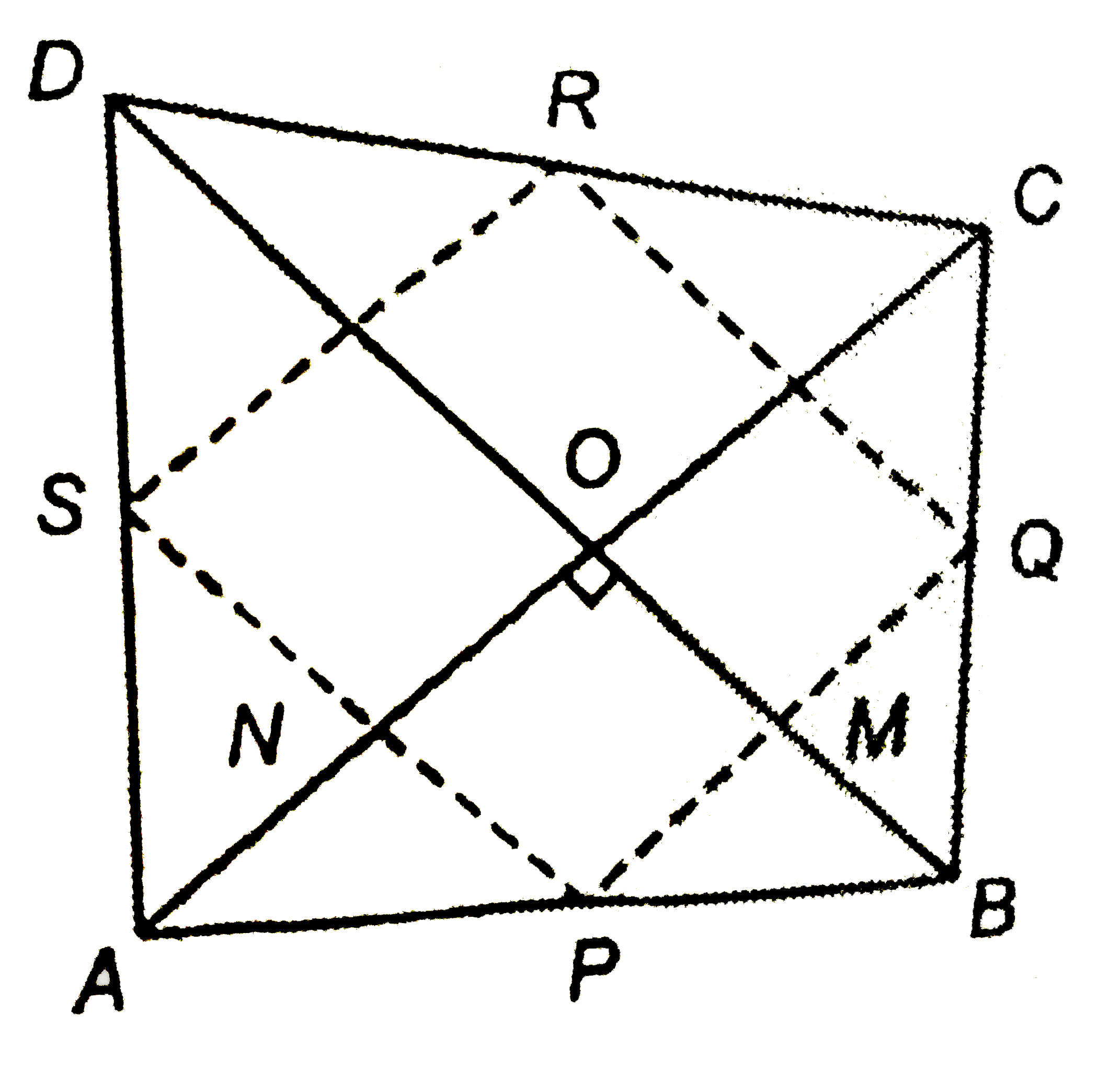
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
Step by step video & image solution for Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
Similar Questions
Show that the quadrialteral formed by joining the mid-points of the consecutive sides of a rhombus, is a rectangle.
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.
 View Solution
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View SolutionThe diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
View SolutionThe diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square, is also a square.
View SolutionProve that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR ABCD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View Solution


