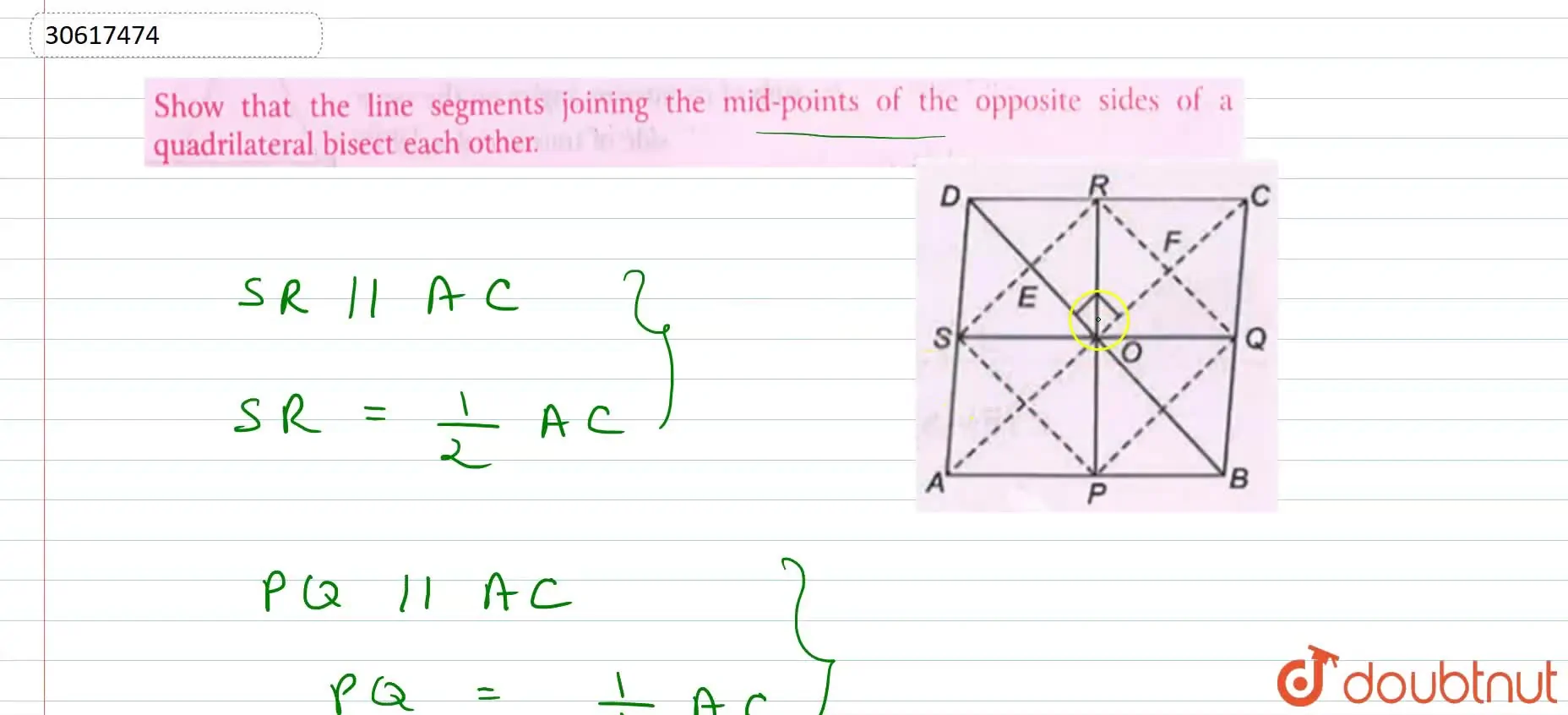
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Let ABCD is a quadrilateral and P,Q,R and S are the mid-points of the sides AB,BC,Co and DA, respectively. i.e., AS = AP= BP, BQ=CQ and CR = DR. We have to show have to show that PR and SQ bisect each other i.e., SO= OQ and PO = OR.
Now, in ΔABD,SandR are mid-points of AD and CD. We known that, the line seginent joining jthe mid-points of two sides of a triangles is parallel to the third side.
∴ SR||ACandSR=12AC (by mid-point theorem)...(1)
Similarly, in ΔABC,PandQ are mid-points of AB and BC
∴ PQ||ACandPQ=12AC (by mid-point theorem)...(2)
From (1) and (2) we, get
PQ||SRandPQ=SR=12AC
∴ Quadrilateral PQRS is a parallelogram whose diagonals are SQ and PR. Also we know that diagonals of a parallelogram bisect each other. So, SQ and PR bisect each other.
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a29videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b15videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (long Answer Questions)5videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise10videos
STATISTICS
Similar Questions
Show that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
View SolutionShow that the lines joining the mid-points of opposite sides of a quadrilateral bisect each other.
View SolutionProve that line joining the midpoints of opposite sides of a quadrilateral bisect each other.
View SolutionThe line segments joining the midpoints of the adjacent sides of a quadrilateral form
View SolutionUsing vector method, prove that the line segments joining the mid-points of the adjacent sides of a quadrilateral taken in order form a parallelogram.
View SolutionProve that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
View Solutioni. Show that the lines joining the vertices of a tetrahedron to the centroids of opposite faces are concurrent.
ii. Show that the joins of the midpoints of the opposite edges of a tetrahedron intersect and bisect each other.View SolutionProve that the lines joining the middle points of opposite sides of a quadrilateral and the line joining the middle points of its diagonals meet in a point and bisect one another.
View SolutionProve that the line segments joints joining the mid-points of the adjacent sides of a quadrilateral from a parallelogram.
View SolutionConsider the - following statements in respect of a quadrilateral :
1. The line segments joining the midpoints of the two pairs of opposite sides bisect each other at the point of intersection.
2. The area of the quadrilateral formed by joining the midpoints of the four adjacent sides is half of the total area of the quadrilateral.
Which of the statements given above is/are correct ?View Solution