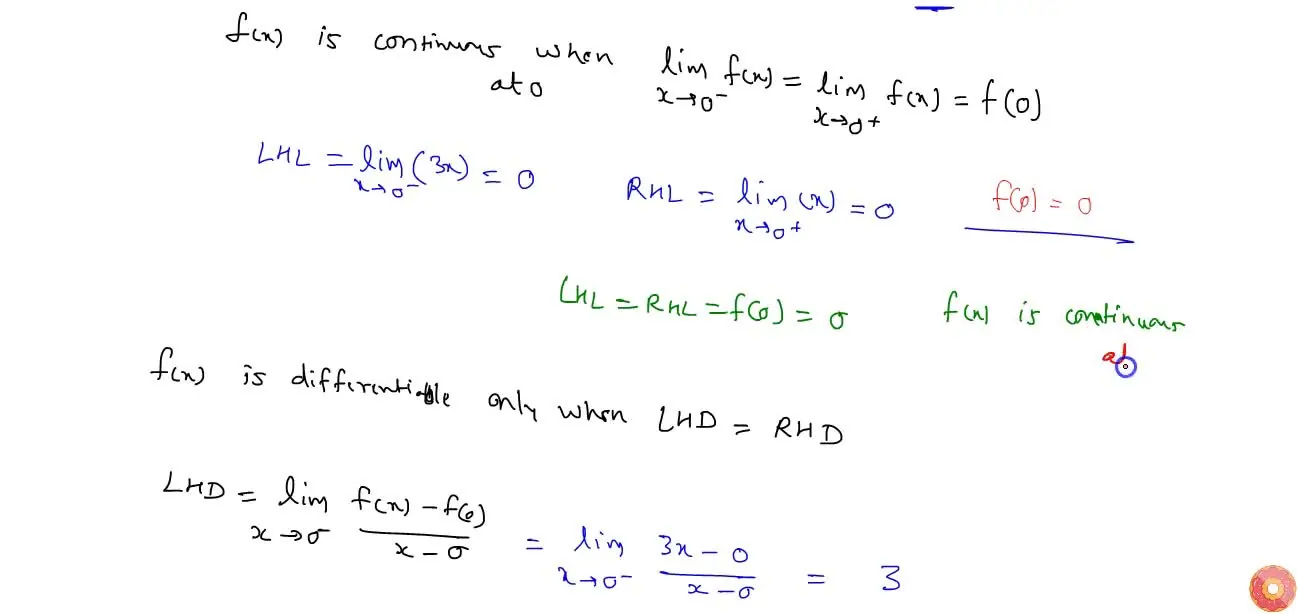Show that the function f(x)=2x−|x| is continuous but not differentiable at x=0
Video Solution
Text Solution
f(x)=2x−x,x≥0
f(x)=2x−(−x),x<0
f(x) is continuous when lim f(x)=limf(x)=f(0)
LHL=limx→0−(3x)=0
RHL=limx→0+=0
f(0)=0
f(x) is differential only when LHD=RHD
LHD=limx→o−f(x)−f(0)x−0=limx→0−(3x−0x−0)=3
RHD=limx→0+(f(x)−f(0)x−0)=limx→0+(x−0x−0)=1
LHD≠RHD
f(x) is not differential at x=0.
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Show that the function f(x)=2x−|x| is continuous at x=0
View SolutionShow that the function f(x)=2x−|x| is continuous at x=0.
View SolutionShow that the function f(x)=|x-2| is continuous but not differentiable at x=2.
View SolutionShow that the function f(x)={|2x−3|[x]x≤0 and sin(πx2),x>0 is continuous but not differentiable at x=0
View SolutionShow that the function f(x)=2x−|x| is continuous at x=0 .
View SolutionShow that the function f(x)=|x−3|, x∈ ∣R, is continuous but not differentiable at x=3.
View Solutionshow that f(x) =|x| is continuous but not differentiable at x =0
View SolutionProve that the function f(x)=2x−|x| is continuous at x=0.
View SolutionShow that f(x)=|x−3| is continuous at x=3.
View SolutionShow that f(x)=|x−3| is continuous but not differentiable at x=3 .
View Solution