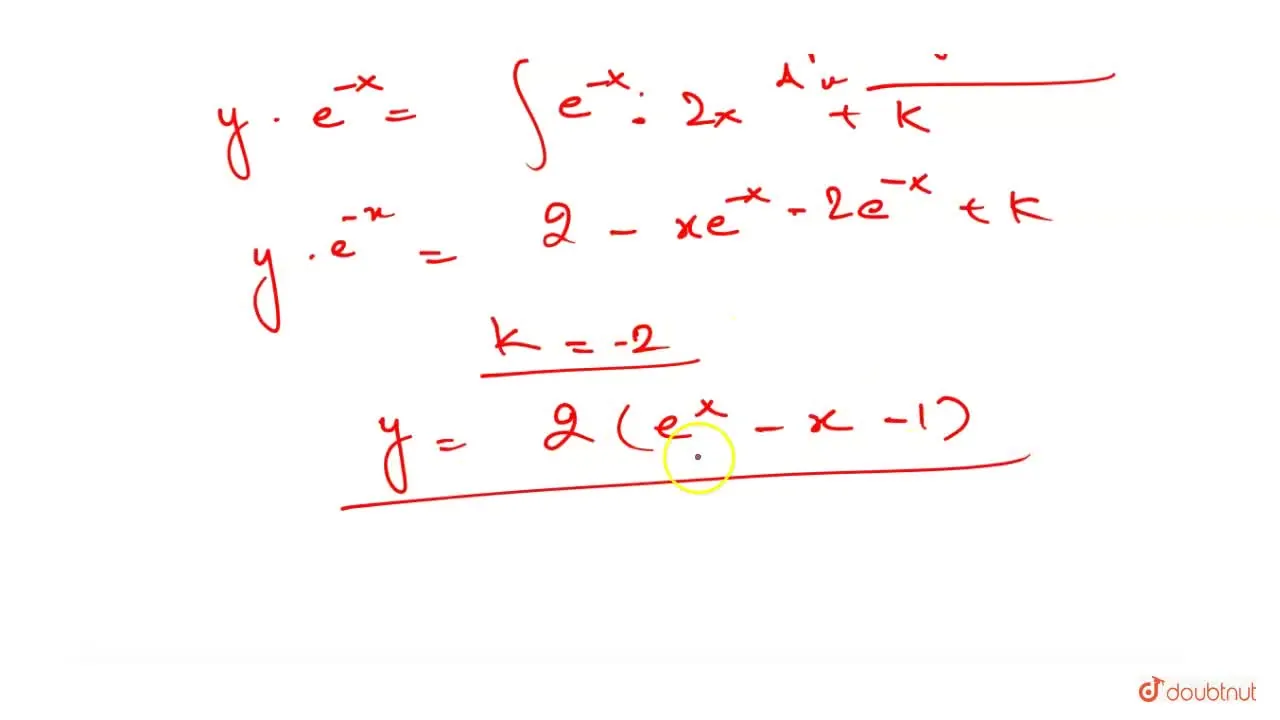Show that the equation of the curve whose slope at any point is equal to y + 2x and which passes through the origin is .
We have ,
Multiplying the equation by IF and integrating
, k being the constant of integration.
, using integration by parts
...(i)
As curve (i) passes through (0, 0)
0 = 0 - 2 + k
Thus the curve is
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Try Yourself26videos
DIFFERENTIAL EQUATIONS
- BOOK - AAKASH INSTITUTECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Assignment (Section - A) Competition Level Questions35videos
DIFFERENTIAL EQUATIONS
- BOOK - AAKASH INSTITUTECHAPTER - DETERMINANTS EXERCISE - SECTION - J12videos
DETERMINANTS
- BOOK - AAKASH INSTITUTECHAPTER - INTEGRALSEXERCISE - Try yourself50videos
INTEGRALS
Similar Questions
What is the equation of the curve whose slope at any point is equal to 2x and which passes through the origin?
View SolutionWhat is the equation of the curve whose slope at any point is equal to 2x and which passes through the origin ?
View SolutionShow that the equation of the curve whose slope at any point is equal to y+2x and which passes through the origin is y+2(x+1)=2e2x.
View SolutionWhat is the equation of the curve whose slope any point is equal to 2x and which passes through the origin?
View Solutionshow that the equation of the curve whose slope at any point is equal to y+2x and which passes through the origin is y+2(x+1)=2e2x.
View SolutionThe equation of one of the curves whose slope at any point is equal to y+2xandy(0)=0 is
View SolutionEquation of the curve whose slope at the point (x,y) is -(x + y) / x and which passes through the points (2, 1) is
View SolutionProve that the equation of a curve whose slope at (x,y) is −x+yx and which passes through the point (2,1) is x2+2xy=8
View SolutionFind the equation of the curve whose gradient at (x,y) is y2x and which passes through the point (a,2a).
View SolutionThe equation of the curve, slope of whose tangent at any point (h,k) is 2kh and which passes through the point (1,1) is (i)x2=y (ii)y2=x (iii)x2=2y (iv) y2=2x
View Solution