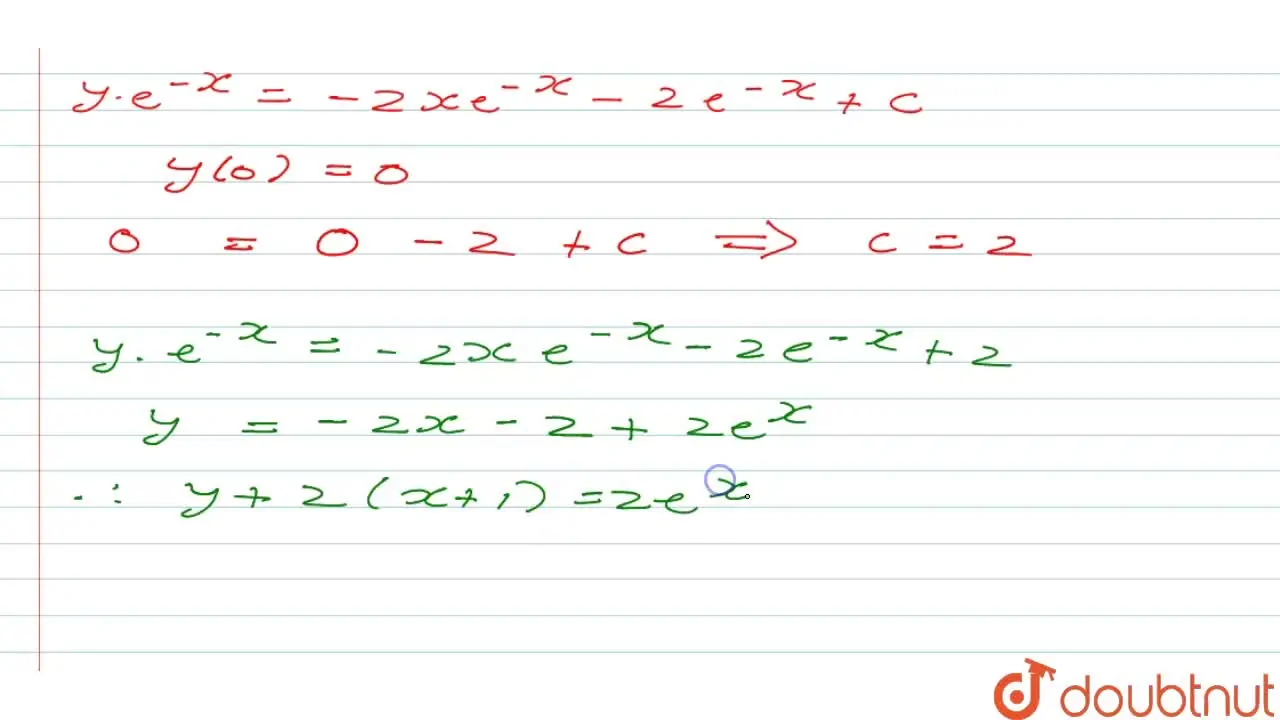Show that the equation of the curve whose slope at any point is equal to y+2x and which passes through the origin is y+2(x+1)=2ex.
Step by step video & image solution for Show that the equation of the curve whose slope at any point is equal to y+2x and which passes through the origin is y+2(x+1)=2e^(x)dot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Prove that the equation of a curve whose slope at (x,y) is −x+yx and which passes through the point (2,1) is x2+2xy=8
View SolutionFind the equation of the curve whose gradient at (x,y) is y2x and which passes through the point (a,2a).
View SolutionThe equation of the curve whose slope is given by dydx=2yx;x>0, y>0 and which passes through the point (1,1) is
View SolutionFind the equation of the curve whose slope at x=0 is 3 and which passes through the point (0,1) satisfying the differential equation (x2+1)d2ydx2=2xdydx.
View SolutionThe slope of the curve y=x3−2x+1 at point x = 1 is equal to :
View SolutionThe equation of one of the curves whose slope of tangent at any point is equal to y+2x is (A) y=2(ex+x−1) (B) y=2(ex−x−1) (C) y=2(ex−x+1) (D) y=2(ex+x+1)
View SolutionFor the curve y=4x3−2x5,find all the points at which the tangent passes through the origin.
View SolutionEquation of the diameter of the circle x2+y2−2x+4y = 0 which passes through the origin is
View SolutionFor the curve y=4x3−2x5 find all points at which the tangent passes through the origin.
View SolutionFor the curve y=4x3−2x5, find all the points at which the tangents pass through the origin.
View Solution