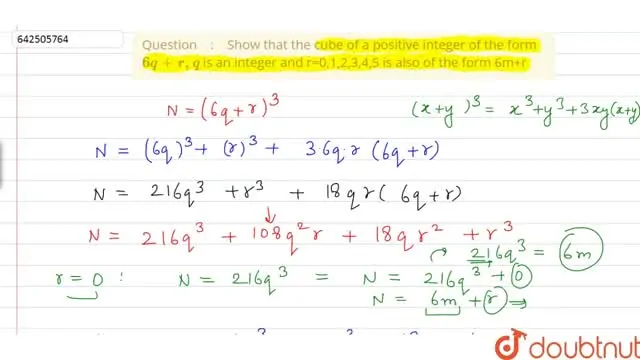
Show that the cube of a positive integer of the form 6q+r,q is an integer and r=0,1,2,3,4,5 is also of the form 6m+r
Let a be an arbitary positive integer. Then, by Euclid division alogorithm, corresponding to the positive intergers 'a' and 6, there exist non negative q and r such that
a=6 q+r ,where, 0≤r<6
⇒a3=(6q+r)3=216q3+r3+3.6q.r(6q+r) [∴(a+b)3=a3+b3+3ab(a+b)]....(i)
⇒a3=(216q3+108q2r+18r2)+r3
where, 0≤r<6
CASE I When r=0, then putting r=0 in Eq.(i), we get
a3=216q3=6(36q3)=6m
Where, m=36q3 is an integer.
CASE II When r=1, then putting r=1 in Eq. (i), we get
a3=(216q3+108q3+18q)+1=6(36q3+18q3+3q)+1
⇒a3=6m+1,wherem=(36q3+18q3+3q) is an integer.
CASE III When r=2, then putting r=2 in Eq. (i) , we get
a216q+216q2+72q+8
a3=(216q3+216q2+72q+6)+2
⇒a3=6(36)q2+12q+1)+2=6m+2
where, m(36q2+36q2+12q+1) is an integer.
CASE IV when r=3, then putting r=3 in Eq. (i), we get
a3=216q3+324q2+162q)+27=(216q3+324q2+162q+24)+3
=6(36q3+54q2+27q+4)+3=6m+3
where, m=(36q2+54q2+27+4) is an integer
CASE V When r=4, then putting r=4 in Eq. (i), we get
a3=(216q2+432q2+288q)+64
=6(36q3+72q2+48q)+60+4
a36(36q3+72q2+48q+10)+4=6m+4
where, m=(36q3+72q2+48q+10) is an integer
CASE VI When r=5, then putting r=5 in Eq. (i), we get
a3=(216q3+540q2+450q)+125
⇒a3=(216q540q2+450q+120+5
⇒a3=6(36q3+90q2+75q+20)+5
⇒a3=6m+5
Where, m=(36q3+90q2+75q+20) is an integer
Hence the cube of a positive integer of hte form 6q+r, q is an integer and r=0,1,2,3,4,5 is also of hte ofrms 6m, 6m+1, 6m+2, 6m+3, 6m+4 and 6m+5 i.e. 6m+r
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - REAL NUMBERSEXERCISE - SHORT ANSWER TYPE QUESTIONS14videos
REAL NUMBERS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRIATIC EQUATIONSEXERCISE - LONG ANSWER TYPE12videos
QUADRIATIC EQUATIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ASWERS QUESTIONS14videos
STATISTICS AND PROBABILITY
Similar Questions
Show that the square of an odd positive integer is of the form 8q+1, for some integer q.
View SolutionShow that the square of an odd positive integer is of the form 8q+1, for some integer q.
View SolutionShow that the square of any positive integer is of the form 3m or, 3m+1 for some integer m .
View SolutionProve that the square of any positive integer of the form 5q+1 is of the same form.
View SolutionProve that the square of any positive integer is of the form 4q or 4q+1 for some integer q .
View SolutionProve that the square of any positive integer is of the form 4q or 4q+1 for some integer q .
View SolutionShow that cube of any positive integer is of the form 4m, 4m+1 or 4m+3, for some integer m.
View SolutionShow that any positive integer is of the form 3q or, 3q+1 or, 3q+2 for some integer q .
View SolutionShow that the square of any positive integer cannot be of the form 5q+2 or 5q+3 for some integer q.
View SolutionProve that the square of any positive integer is of the form 5q,5q+1,5q+4 for some integer q.
View Solution