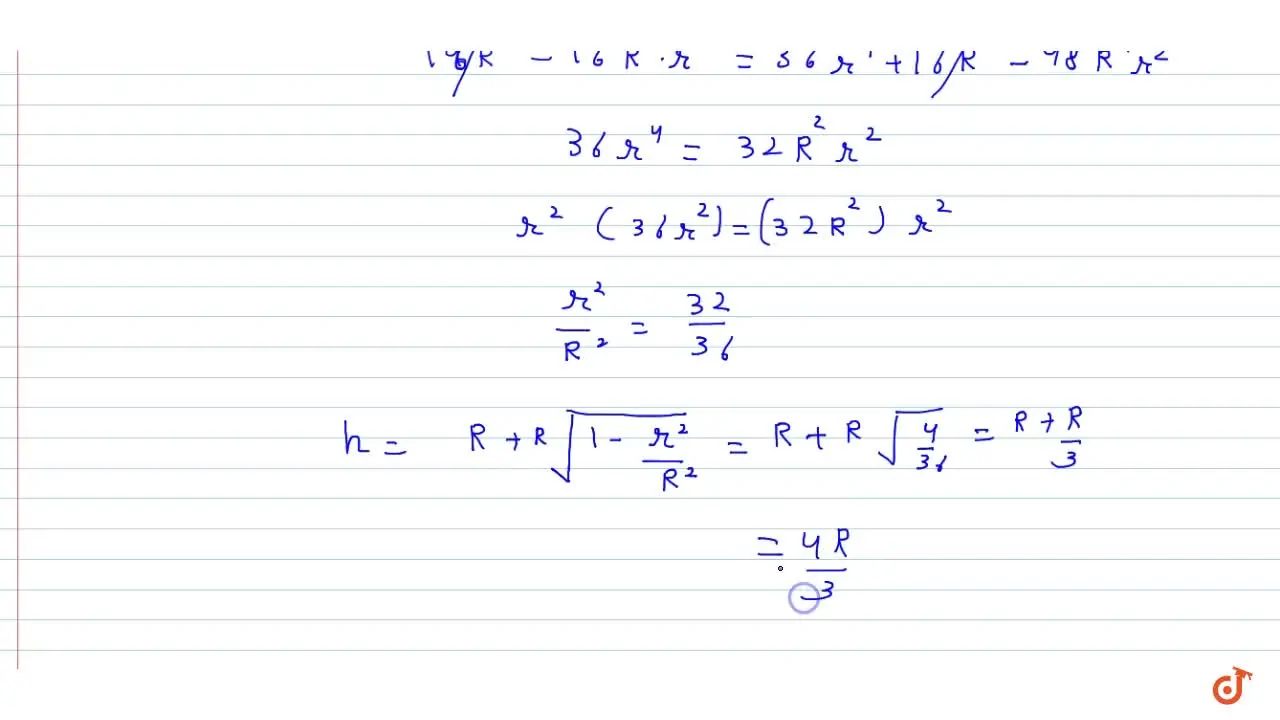Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is 4r3.
A sphere of fixed radius (r) is given.
Let R and h be the radius and the height of the cone respectively.
[XII06_MEX15]
To show h=4r3
In triangleABC, AC=h-r
Therefore, using Pythagoras theorem,
(h−r)2+R2=r2
⇒R2=r2−(h−r)2
Volume of cone:
V=13πR2h
V=13π(r2−(h−r)2)h
V=13π(r2−h2−r2+2hr)h
V=13π(2h2r−h3)
For maxima or minima,dVdh=0
Now,dVdh=13π[4hr−3h2]=0
∴4hr=3h2
∴h=4r3
Related Playlists
- BOOK - NCERTCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.49videos
APPLICATION OF DERIVATIVES
- BOOK - NCERTCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.529videos
APPLICATION OF DERIVATIVES
- BOOK - NCERTCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.327videos
APPLICATION OF DERIVATIVES
- BOOK - NCERTCHAPTER - APPLICATION OF INTEGRALSEXERCISE - EXERCISE 8.27videos
APPLICATION OF INTEGRALS
Similar Questions
Show that the altitude of the right circulau cone of maximum volume that can be inscribed in a sphere of radius r is 4r3. also show that the maximum volume of cone is 827 of the volume of the sphere.
View SolutionShow that the altitude of a right circular cone of maximum volume that can be inscribed in a sphere of radius r is 4r/3..
View SolutionShow that the radius of right - circular cylinder of maximum volume, that can be inscribed in a sphere of radius 18 cm, is 6√6cm.
View SolutionFind the height of right circular cylinder of maximum volume that can be inscribed in a sphere of radius 10√3cm.
View SolutionShow that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R√3 .
View SolutionThe altitude of a right circular cone of minimum volume circumscribed about a sphere of radius r is
View SolutionShow that the height of the cone of maximum volume that can be inscribed in a sphere of radius 12cm is 16cm.
View SolutionShow that the height of the cone of maximum vvolume that can be inscribed in a sphere of radius 12 cm is 16 cm.
View SolutionThe height of a right circular cylinder of maxium volume inscirbed in a sphere of radius 3 is
View SolutionThe radius of the cylinder of maximum volume, which can be inscribed in a sphere of radius R is
View Solution