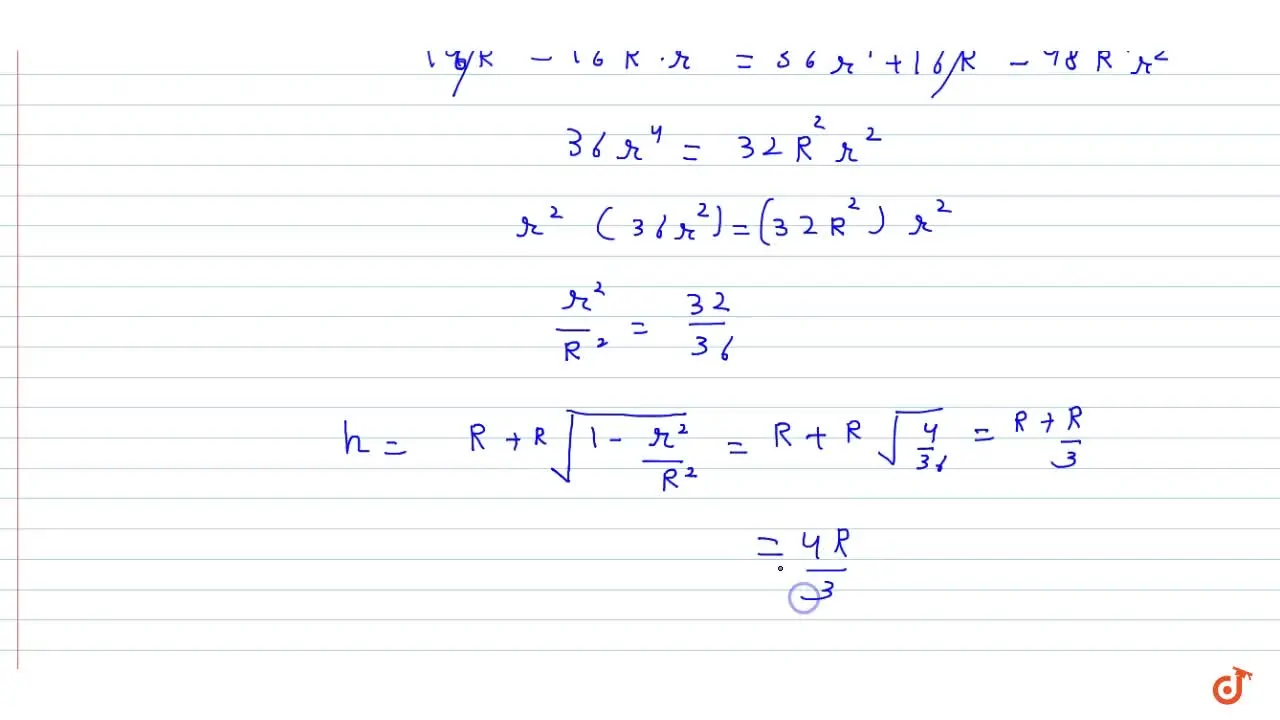Show that the altitude of a right circular cone of maximum volume that can be inscribed in a sphere of radius r is 4r/3..
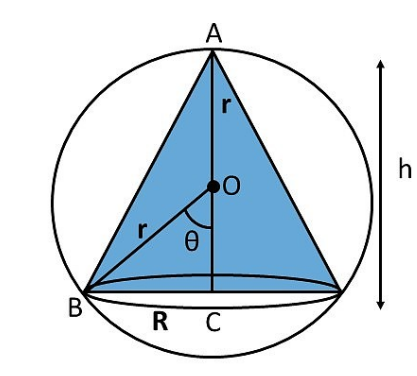
Let Rand h be the radius and height of the cone
r be the radius of sphere
To show h=4r3
Volume of sphere
In △ABC,AC=h−r
Therefore , using pythagoras theorem
(h−r)2+R2=r2
⇒R2=r2−(h−r)2
Volume of cone :V=13πR2h or V=13π(r2−(h−r)2h)
=13π[r2−h2−r2+2hr]h
=13π[2h2r−h3]
For maxima and minima dVdh=0
Now, dVdh=13π[4hr−3h2]
putting (dV)(dh)=0
we get
4hr=3h2
h=4r3
d2Vdh2=13π[4r−6h]
Putting h=4r3
d2Vdh2=13π[4r−6.4r3]⇒−13π[4r]
which is less than zero, therefore h=4r3 is a maxima and the volume of the cone at h will be maximum
Related Playlists
- BOOK - NCERTCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.327videos
APPLICATION OF DERIVATIVES
- BOOK - NCERTCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - MISCELLANEOUS EXERCISE23videos
APPLICATION OF DERIVATIVES
- BOOK - NCERTCHAPTER - APPLICATION OF INTEGRALSEXERCISE - EXERCISE 8.27videos
APPLICATION OF INTEGRALS
Similar Questions
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is 4r3.
View SolutionThe altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is
View SolutionThe altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is
View SolutionShow that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is 4R3. Also find maximum volume in terms of volume of the sphere.
View SolutionShow that the altitude of the right circulau cone of maximum volume that can be inscribed in a sphere of radius r is 4r3. also show that the maximum volume of cone is 827 of the volume of the sphere.
View SolutionShow that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius R is 4R3.
View SolutionShow that the radius of right - circular cylinder of maximum volume, that can be inscribed in a sphere of radius 18 cm, is 6√6cm.
View SolutionThe altitude of a right circular cone of minimum volume circumscribed about a sphere of radius r is
View SolutionFind the height of right circular cylinder of maximum volume that can be inscribed in a sphere of radius 10√3cm.
View SolutionThe height of a right circular cylinder of maxium volume inscirbed in a sphere of radius 3 is
View Solution