Show that no three consecutive binomial coefficients can be in (i) G.P., (ii) H.P.
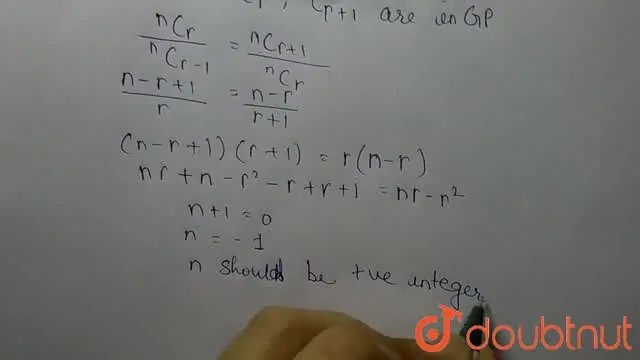
Suppose that the r th, (r + 1) th and (r + 2) th
coefficients of (1+x)n are in GP .
i.e., nCr−1,nCr,nCr+1 are in GP .
Then nCrnCr−1=nCr+1nCr
⇒n−r+1r=n−rr+1[∵nCrnCr−1=n−r+1r]
⇒(n−r+1)(r+1)=r(n−r)
⇒nr+n−r2−r+r+1=nr−r2
⇒n+1=0
⇒n=−1
which is not possible , since n is a positive integer.
Related Playlists
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - JEE Type Solved Example : (Matching Type Questions )2videos
BIONOMIAL THEOREM
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise For Session 17videos
BIONOMIAL THEOREM
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)23videos
AREA OF BOUNDED REGIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)16videos
CIRCLE
Similar Questions
Show that no three consecutive binomial coefficients can be in G.P.
View SolutionStatement 1:Three consecutive binomial coefficients are always in A.P. Statement 2: Three consecutive binomial coefficients are not in H.P.
View SolutionShow that the roots of the equation ax2+2bx+c=0 are real and unequal whre a,b,c are the three consecutive coefficients in any binomial expansion with positive integral index.
View SolutionIf some three consecutive coefficeints in the binomial expanison of (x+1)n in powers of x are in the ratio 2 : 15 : 70, then the average of these three coefficients is
View SolutionIf some three consecutive coefficeints in the binomial expanison of (x+1)n in powers of x are in the ratio 2 : 15 : 70, then the average of these three coefficients is
View SolutionIf some three consecutive coefficeints in the binomial expanison of (x+1)n in powers of x are in the ratio 2 : 15 : 70, then the average of these three coefficients is
View SolutionFind k such that k+9, k−6 and 4 form three consecutive terms of a G.P.
View SolutionIf the square of differences of three numbers be in A.P., then their differences re in (A) A.P. (B) G.P. (C) H.P. (D) none of these
View SolutionIf the four consecutive coefficients in any binomial expansion be a, b, c, d, then prove that (i) a+ba,b+cb,c+dc are in H.P. (ii) (bc+ad)(b−c)=2(ac2−b2d)
View SolutionIf the four consecutive coefficients in any binomial expansion be a, b, c, d, then prove that (i) a+ba,b+cb,c+dc are in H.P. (ii) (bc+ad)(b−c)=2(ac2−b2d)
View Solution