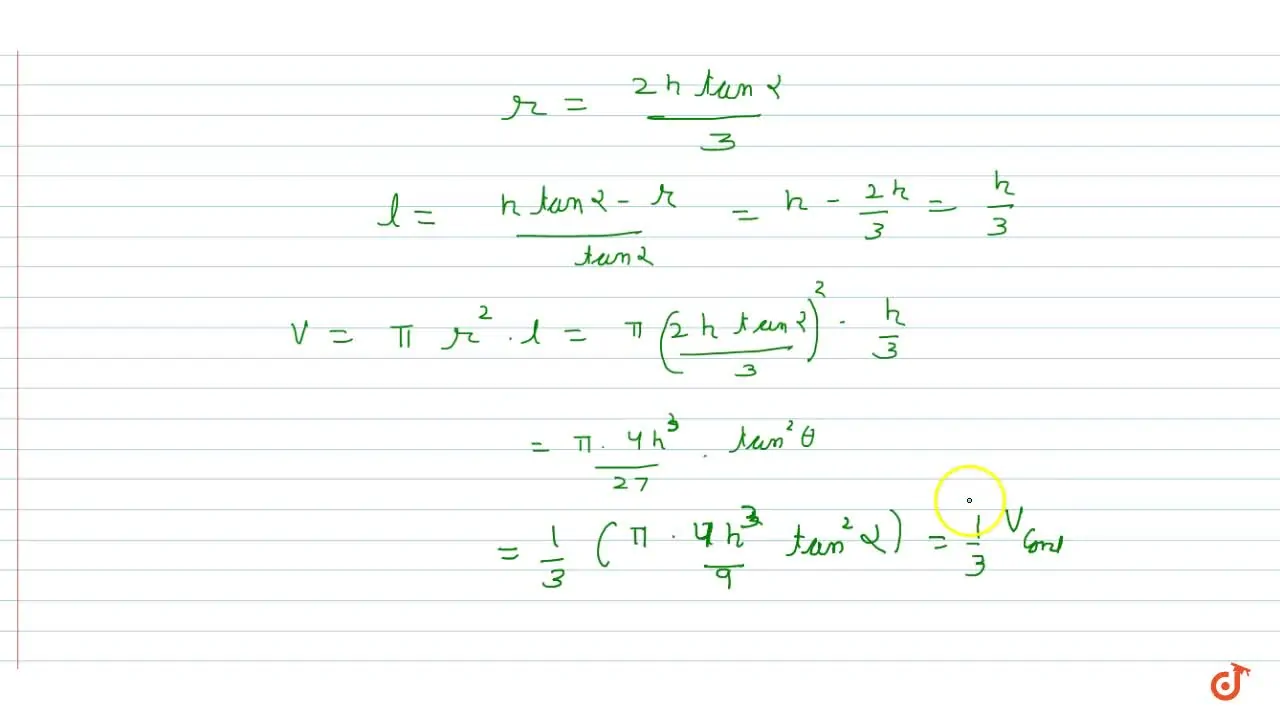Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical angle is one-third that of the cone and the greatest volume of cylinder is 427πh3tan2α.
The given right circular cone of fixed height (h) and semi-vertical angle (α) can be drawn as:

Here, a cylinder of radius R and height H is inscribed in the cone.
We have r=tanhα
Now since ΔAOG is similar to tra∈g≤CEG, we have
AOOG=CEEG
⇒hr=Hr−R
⇒H=hr(r−R)=1tanα(htanα−R)
Now the volume V of the cylinder is given by
V=πR2H=πR2hr(r−R)=1tanα(htanα−R)=1tanα(htanα−R)
dVdR=2πRh−3πR2tanα
Now, dVdR=0
∴2πRh−3πR2tanα=0
⇒R=2htanα3
Now,d2VdR2=2πh−6πRtanα
=2πh−6π(2htanα3)tanα=−2πh<0
By second derivative test, the volume of the cylinder is the greatest when R=2htanα3
Now, when R=2htanα3H=1tanα(htanα−2htanα3)=h3
Thus, the height of the cylinder is one-third the height of the cone when the volume of the cylinder is the greatest. Now, the maximum volume of the cylinder can be obtained as:
=π(2htanα3)2(h3)=427πh3tan2α
Related Playlists
- BOOK - NCERTCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.49videos
APPLICATION OF DERIVATIVES
- BOOK - NCERTCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.529videos
APPLICATION OF DERIVATIVES
- BOOK - NCERTCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.327videos
APPLICATION OF DERIVATIVES
- BOOK - NCERTCHAPTER - APPLICATION OF INTEGRALSEXERCISE - EXERCISE 8.27videos
APPLICATION OF INTEGRALS
Similar Questions
Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical angle is one-third that of the cone and the greatest volume of cylinder is 427πh3tan2α.
View SolutionThe volume of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical angle α is kπh3tan2α, then 6k=
View SolutionThe height of the cylinder of the greatest volume that can be inscribed in a sphere of radius 3 is
View SolutionShow that the height of the cylinder of maximum volume that can be inscribed in a cone of height h is 13h
View SolutionShow that the volume of the greatest cylinder, which can be inscribed in a cone of height 'h' and semi - vertical angle 30∘ is 481πh3
View SolutionShow that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R√3 .
View SolutionThe radius of cylinder of maximum volumne which can be inscribed in a right circular cone of radius R and height H ( axis of cylinder and cone are same ) H given by
View SolutionA right circular cylinder of maximum volume is inscribed in a given right circular cone of height h and base radius r, then radius of cylinder is:
View SolutionShow that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to 2/3 of the diameter of the sphere.
View SolutionA metallic cylinder of radius 8 cm and height 2 cm is melted and converted into a right circular cone of height 6 cm . The radius of the base of this cone is
View Solution