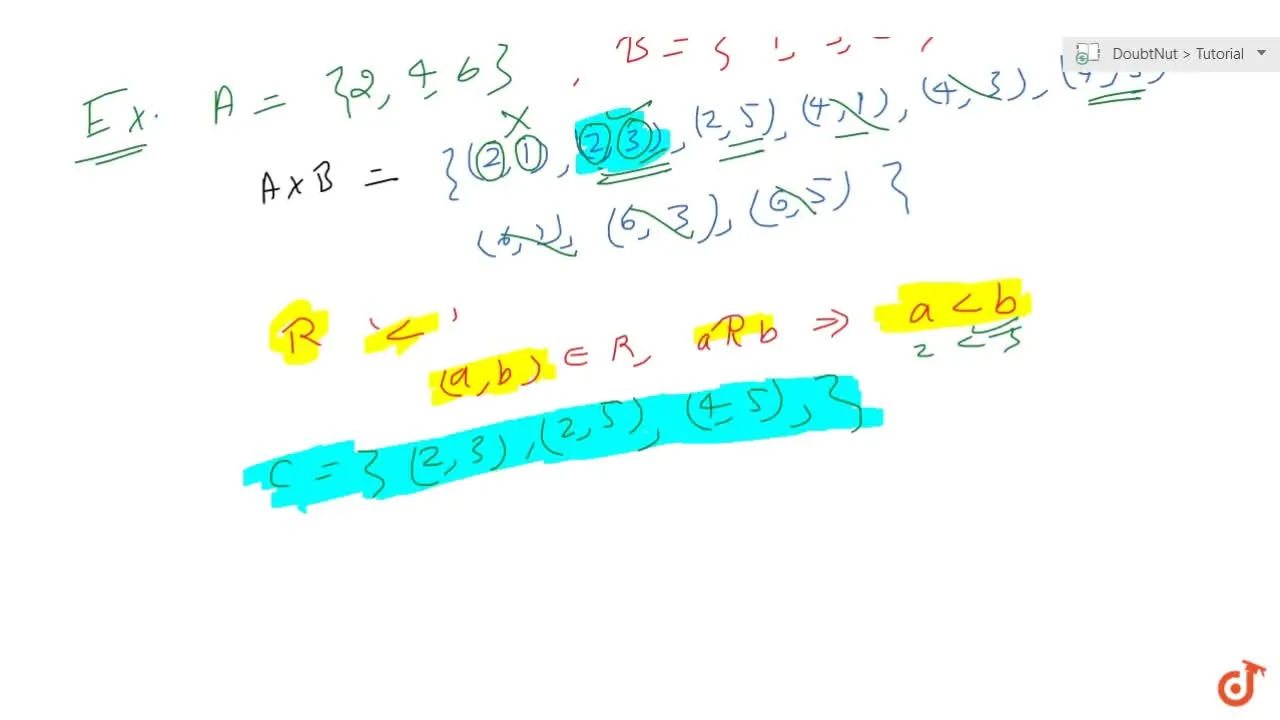Relation on a set
What is Relation on a set?
Relations and its types are one of the critical algebra topics in mathematics. It should be noted that there are different concepts which are related to relations
What are Relations?
In mathematical concepts, Relation is the relationship between two different sets of information. If we consider two sets, then the relation between them will be established provided that there is a connection between the elements of two or more non-empty sets.
So, it can be said that a set of ordered pairs is defined as a relation.
What is Reflexive Relation on a set?
A relation ‘R’ in a set ‘A’ is called reflexive, if (a, a) belongs to R, for every 'a' that belongs to A.
Let R be the relation defined in a set A.
If (a, a) ∈ R for every a ∈ A then R is set to be reflexive. Here, in every element of A is R-related to itself, or it can be said that aRa for all a ∈ A.
A relation R in set A is not reflexive, if there is at least an element a ∈ A in a form that (a, a) ∉ R.
For example, set A = {p, q, r, s}.
The relation R1= {(p, p), (p, r), (q, q), (r, r), (r, s), (s, s)} in A is reflexive, as each element in A is R1 related to itself.
But the relation R2= {(p, p), (p, r), (q, r), (q, s), (r, s)} is not reflexive in set A, since q, r, s ∈ A; however (q, q) ∉ R2, (r, r) ∉ R2 and (s, s) ∉ R2
Solved Example of Reflexive Relation on Set
1) A relation R is defined on the set Z (set of all integers) by “aRb if and only if 2a + 3b is divisible by 5”, for all a, b ∈ Z. Find out whether R is a reflexive relation on Z.
Solution:
Let a ∈ Z. Now 2a + 3a = 5a, which is divisible by 5. Thus aRa holds for all a in Z i.e. R is reflexive.
2) A relation R is defined on the set Z by “aRb if a – b is divisible by 5” for a, b ∈ Z. Find out whether R is a reflexive relation on Z.
Solution:
Let a ∈ Z. Then a – a is divisible by 5. Thus aRa holds for all a in Z i.e. R is reflexive.
3) Consider the set Z in which a relation R is defined by ‘aRb if and only if a + 3b is divisible by 4, for a, b ∈ Z. Prove that R is a reflexive relation on set Z.
Solution:
Let a ∈ Z. Now a + 3a = 4a, which is divisible by 4. Thus aRa holds for all a in Z i.e. R is reflexive.
4) On the set of all real numbers R, a relation ρ is defined by ‘xρy’ if and only if |x – y| ≤ y, for x, y ∈ R. Prove that the ρ is not reflexive relation.
Solution:
The relation ρ is not reflexive as x = -2 ∈ R but |x – x| = 0 which is not less than -2(= x).
Similar Questions
The union of two equivalence relations on a set is not necessarily an equivalence relation on the set.
View SolutionThe union of two equivalence relations on a set is not necessarily an equivalence relation on the set.
View SolutionIf the numbers of different reflexive relations on a set A is equal to the number of different symmetric relations on set A, then the number of elements in A is
View SolutionIf R and S are transitive relations on a set A , then prove that R∪S may not be a transitive relation on A .
View SolutionIf R and S are transitive relations on a set A, then prove that R∪S may not be a transitive relation on A.
View SolutionIf R and S are two equivalence relations on a set A; then R∩S is also an equivalence relation on R.
View SolutionLet R and S be two non-void relations on a set A. Which of the following statements is false?
View SolutionLet R1 and R2 be equivalence relations on a set A, then R1∪R2 may or may not be
View SolutionA relation in a set A is called ......... relation, if each element of A is related to itself.
View SolutionThe number of reflexive relation of a set with four elements is equal to :
View Solution