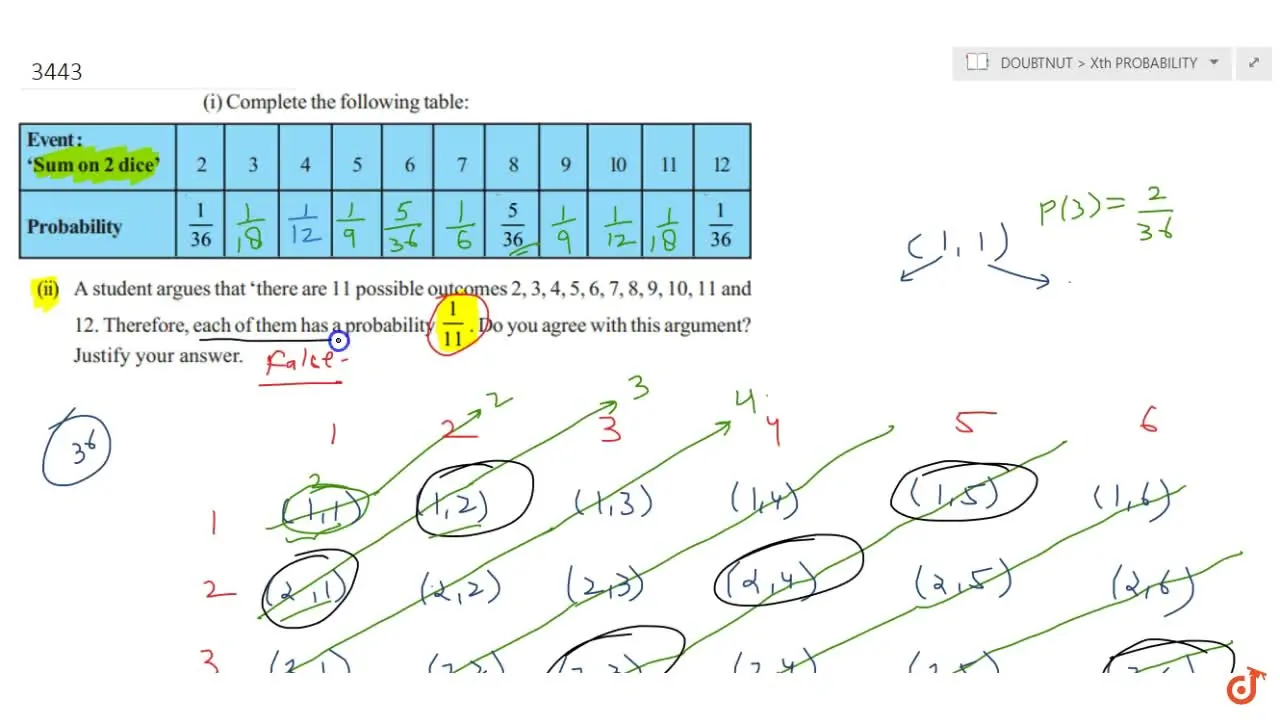
Refer to Example 13. (i) Complete the following table (ii) A student argues that 'there are 11 possible outcomes 2,3,4,5,6,7.8,9,10,11 and 12. Therefore, each of them has a probability 111. Do you agree with this argument? Justify
When two dice are rolled, then their sum can be between 2 to 12.
Here, total number of possible outcomes,n(S)=6∗6=36
When sum is 2, possible outcomes are,
S2=(1,1)
So,P(S2)=136
When sum is 3, possible outcomes are,
S3={(1,2),(2,1)}
So,P(S3)=236=118
When sum is 4, possible outcomes are,
S4={(1,3),(3,1),(2,2)}
So,P(S4)=336=112
When sum is 5, possible outcomes are,
S5={(1,4),(4,1),(2,3),(3,2)}
So,P(S5)=436=19
When sum is 6, possible outcomes are,
S6={(1,5),(5,1),(3,3),(4,2),(2,4)}
So,P(S6)=536
When sum is 7, possible outcomes are,
S7={(1,6),(6,1),(4,3),(5,2),(2,5),(3,4)}
So,P(S7)=636=16
When sum is 8, possible outcomes are,
S8={(2,6),(6,2),(5,3),(3,5),(4,4)}
So,P(S8)=536
When sum is 9, possible outcomes are,
S9={(3,6),(6,3),(5,4),(4,5)}
So,P(S9)=436=19
When sum is 10, possible outcomes are,
S10={(4,6),(6,4),(5,5)}
So,P(S10)=336=112
When sum is 11, possible outcomes are,
S11={(5,6),(6,5)}
So,P(S11)=236=118
When sum is 12, possible outcomes are,
S12={(6,6)}
So,P(S12)=136
So, with the above values we can complete the given table.
(ii) As the student argues that probability of each sum is same, he is incorrect as we have shown above each of these values are not identical and not equal to 111.
Related Playlists
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - Exercise 15.25videos
PROBABILITY
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - SOLVED EXAMPLES13videos
PROBABILITY
- BOOK - NCERTCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.45videos
POLYNOMIALS
- BOOK - NCERTCHAPTER - QUADRATIC EQUATIONSEXERCISE - EXERCISE 4.26videos
QUADRATIC EQUATIONS
Similar Questions
Refer to Example 13. (i) Complete the following table (ii) A student argues that 'there are 11 possible outcomes 2,3,4,5,6,7.8,9,10,11 and 12. Therefore, each of them has a probability 111. Do you agree with this argument? Justify
View SolutionTwo dice, one blue and one grey, are thrown at the same time. Complete the following table: Event: Sum on two dice, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 Probability, , , , , , , , , , , From the above table a student argues that there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of them has a probability 111 . Do you agree with this argument?
View SolutionIf U={4,5,6,7,8,9,10,11,12} and C={4,6,8,10,12 } then find U-C .
View SolutionIf U = {set of natural numbers} and A = {set of even natural numbers} , then find A' .
View SolutionFind the median of the given data 11,12,13,14,5,7,9,6,4,1
View SolutionIf AΔB={1,2,3,4,5,6,7,8,9,11,13} and B={4,5,6,8,11,13} then find A.
View SolutionFind the order of the matrix .
⎡⎢⎣74612001761144⎤⎥⎦View SolutionFind the value of if the mean of the following distribution is 7.5. 3 5 7 9 11 13 6 8 15 8 4
View SolutionArrange the following fractions in ascending order:
(i)34,56,79,1112
(ii)45,710,1115,1720View SolutionA game consists fo spining an arrow which come to rest pointing at one of the number 1,2,3,4,5,6,7,8,9, 10,11,12. Find the probability that the point at (i) a prime number, (ii) a number less than or equal to 9, (iii) a number between 3 and 11.
View Solution