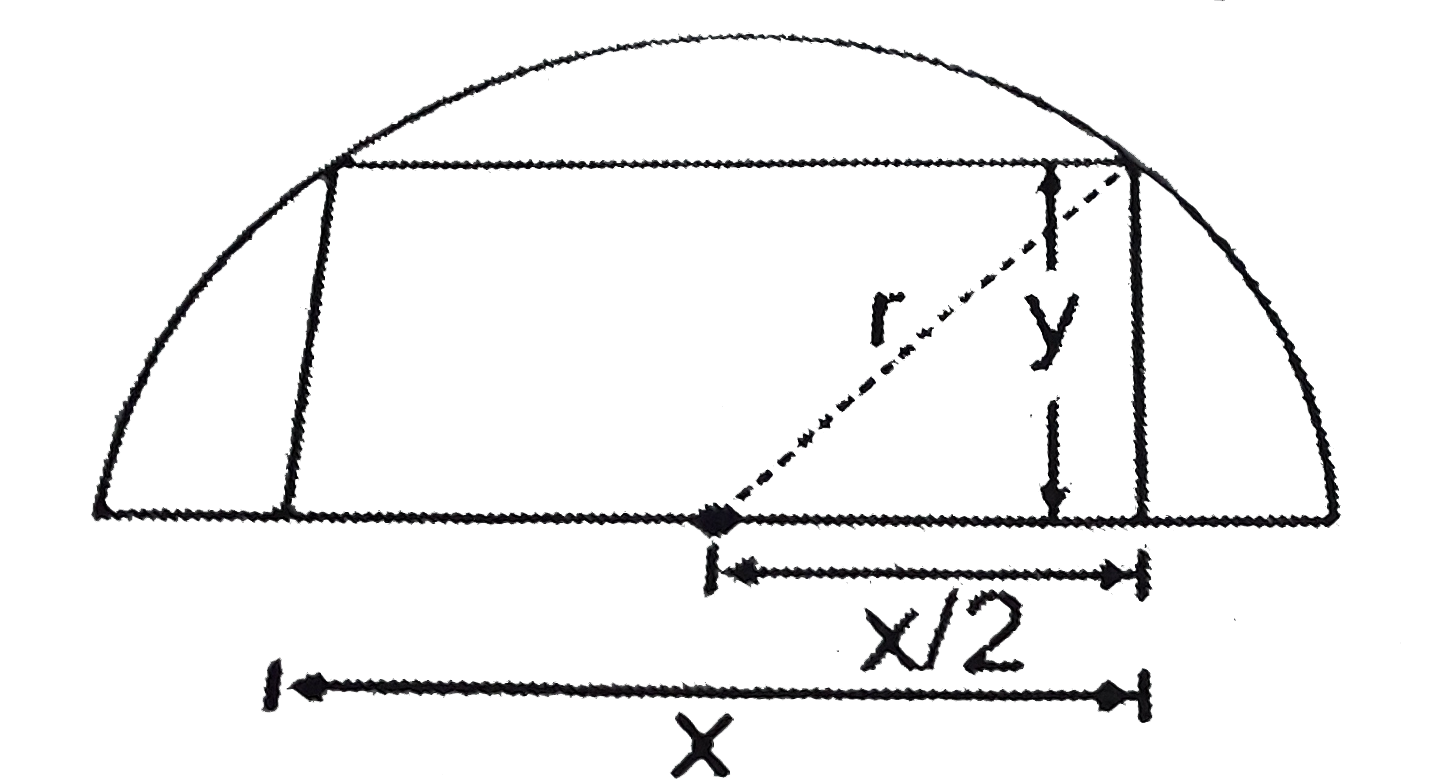
Rectangles are inscribed inside a semicircle of radius r. Find the rectangle with maximum area.
Let sides of rectangle be x and y (as show in figure).
⇒ A=xy
Hence x and y are not independent variables and are related by Pythogorus theorem with r.
x24+y2=r2 rArr y=√r2−x24
⇒ A(x)=x√x2−x24
⇒ A(x)=√x2r2−x44
Let f(x)=r2x2−x44, x∈(0,r)
A(x) is maximum when f(x) is maximum
Hence f(x)=x(2r2−x2)=0 ⇒ x=r√2
also f(r√2)<0 and f(r√2)>0
confirming at f(x) is maximum when x =r √2&y=r√2.
Related Playlists
- BOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Self Practice Problems34videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise -1A5videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCECHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)8videos
COMBINATORICS
Similar Questions
Rectangles are inscribed inside a semi-circle of radius r. Find the rectangle with maximum area.
View Solutionrectangles are inscribed in a circle of radius r the dimensions of the rectangle which has the maximum area are
View Solutionrectangles are inscribed in a circle of radius r the dimensions of the rectangle which has the maximum area are
View SolutionA rectangle in inscribed in a circle of radius 5 cm. if the breadth of the rectangle is 6 cm. then find the length of the rectangle.
View SolutionA rectangle is inscribed in a semicircle of radius 1 unit. If its two vertices lie on the diameter, for largest size, then its dimensions are
View SolutionA reactangle with one side 4 cm is inscribed in a circle of radius 2.5 cm. Find the area of the rectangle
View SolutionA rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. Find the dimensions of rectangle so that the area is maximum. Find the area also.
View SolutionA rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. Find the dimensions of the rectangle so that its area is maximum. Find also the area.
View SolutionFind the ratio of the area of a square inscribed in a semi-circle of radius r to the area of another square inscribed in the entire circle of radius r.
View SolutionA rectangle of maximum area is drawn inside a circle of diameter 5 cm. What is the maximum area of such a rectangle?
View Solution


