Real Numbers

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

Real Numbers

The combination of rational and irrational numbers is known as real numbers. All these numbers can be represented in the number line where all the arithmetic operations can also be performed on these numbers as well. Here, in this chapter, we will focus on real number definition, real number properties along with real number example.

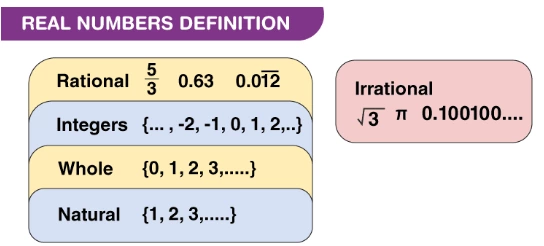
Rational Number

Real Numbers Definition

Real numbers are defined as the union of both the rational as well as the irrational numbers. It should be noted that they are both positive and negative. They are denoted by the symbol “R”. Under this category, all the natural numbers, fraction, and decimals are included. We will have a look at the below figure where it shows the classification of real numerals.

Set of Real Numbers

Different categories include whole and natural numbers in the set of real numbers.  You can check the table below:

Category

Definition

Example

Natural Numbers

It contains all counting number that start from 1. N = {1,2,3,4,……}

All the numbers like 1, 2, 3, 4,5,6,…..

Whole Numbers

It is a collection of zero and natural number. W = {0,1,2,3,…..}

All the numbers that also include 0 like 0, 1, 2, 3, 4,5,6,…..…

Integers

It is the collective result of whole numbers as well as negative of all natural numbers.

It includes -infinity (-∞),……..-4, -3, -2, -1, 0, 1, 2, 3, 4, ……+infinity (+∞)

Rational Numbers

These are numbers that can be written in the form of p/q, where q≠0.

Some examples of rational numbers are ½, 5/4 and 12/6 etc.

Irrational Numbers

All the numbers that are not rational and also cannot be written in the form of p/q.

Irrational numbers are non-terminating and non-repeating in nature like √2

Real Numbers Chart

Below is the real number chart where you can find all the types:

Rational number

Properties of Real Numbers

When it comes to the properties of real numbers, there are four main properties which include commutative property, associative property, distributive property, and identity property. Consider “p, q and r” are the real numbers. On the basis of these properties, we can define the numbers as;

Commutative Property

If p and q are the numbers, then the general form will be p + q = q + p for addition and p.q = q.p for multiplication.

Addition: p + q = q + p. For example, 4 + 3 = 3 + 4, 2 + 3 = 3 + 2

Multiplication: p x q = q x p. For example, 4 × 3 = 3 × 4, 2 × 4 = 4 × 2

Associative Property

If p, q and r are the numbers, then the general form will be p + (q + r) = (p + q) + r for addition(pq) r = p (qr) for multiplication.

Addition: The general form will be p + (q + r) = (p + q) + r. An example of additive associative property is 7 + (4 + 2) = (7 + 4) + 2.

Multiplication: (pq) r = p (qr). An example of a multiplicative associative property is (1 × 2) 4 = 1 (2 × 4).

Distributive Property

For three numbers p, q, and r, which are real in nature, the distributive property is in the form of :

p (q+ r) = pq + pr and (p + q) r = pr + qr.

Example of distributive property is: 5(3 + 4) = 5 × 3 + 5 × 4. Here, both sides will yield 35.

Identity Property

There are additive and multiplicative identities.

For addition: p + 0 = p. (since zero is additive identity)

For multiplication: a × 1 = 1 × a = a. (1 is multiplicative identity)

Related Videos:

Now, we will check for some solved questions that would prove to be quite helpful.

Problem 1: If two positive integers a and b are written as
a= x3y2  and b=xy3. x, y are prime numbers, then can you find the HCF (a, b)?

  1.  xy
  2.  xy2
  3.  x3y3
  4.  x2y2

Solution: HCF is a common factor between the number. So HCF = xy2 .Hence Option (B).

Problem 2: If two positive integers p and q can be expressed as p = ab2 and q = a3b   a, b being prime numbers, then find LCM (p, q)

(A) ab

(B) a2b2

(C) a3b2

(D) a3b3

Solution:  LCM is Product of the greatest power of each prime factor involved in the number
So LCM=a3b2 .Hence Option (C).

Problem 3: The number of participants in Hindi, English and Mathematics are 60, 84 and 108, in a seminar respectively. Can you calculate the minimum number of rooms required if in each room the same numbers of participants are to be seated where all of them being in the same subject?

Solution:  We need to find the HCF of 60,84 and 108
By prime factorisation
60=2*2*3*5
84=2*2*3*7
108=2*2*3*3*3
HCF =12
Rooms required= 60/12 + 84/12+108/12=5+7+9=21

Problem 4:   The product of three consecutive positive integer is divisible by 6. Can you prove it?

Sol:  Let n be any positive integer. As we know that any positive integer is of the form 6q or 6q + 1 or 6q + 2 or 6q + 3 or 6q + 4, 6q + 5.

If n = 6q, n (n + 1)   (n + 2)  = 6q (6q + 1)   (6q + 2), which is divisible by 6

If n = 6q + 1, n (n + 1)   (n + 2)  = (6q + 1)   (6q + 2)   (6q + 3)

 n (n + 1)   (n + 2)  = 6 (6q + 1)   (3q + 1)   (2q + 1)  Which is divisible by 6

If n = 6q + 2, n (n + 1)   (n + 2)  = (6q + 2)   (6q + 3)   (6q + 4) n (n + 1)   (n + 2)

 = 12 (3q + 1)   (2q + 1)   (2q + 3), which is divisible by 6. So, in the same way, we can prove others as well. Thus it is proved that the product of three consecutive positive integers is divisible by 6. 

Important Chapters:

|