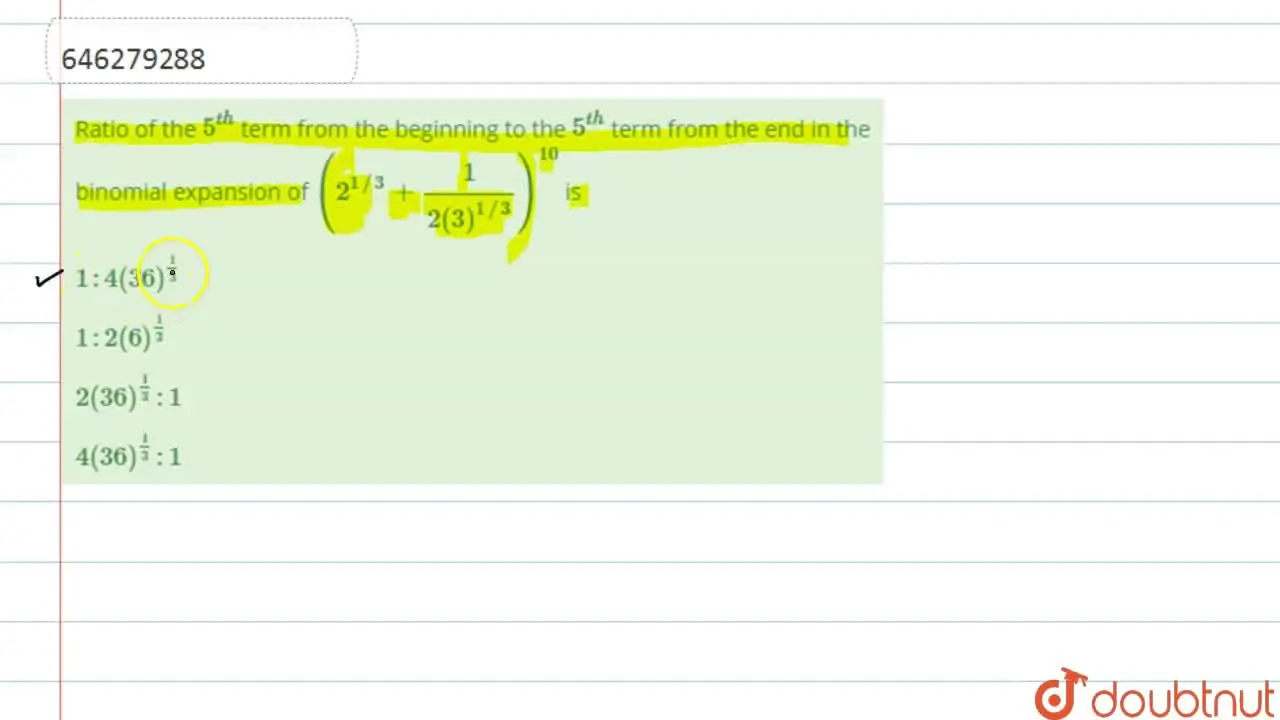
Ratio of the 5th term from the beginning to the 5th term from the end in the binomial expansion of (21/3+12(3)1/3)10 is Solution in Bengali
1:4(36)13
1:2(6)13
2(36)13:1
4(36)13:1
The correct Answer is:D
Step by step video & image solution for Ratio of the 5^(th) term from the beginning to the 5^(th) term from the end in the binomial expansion of (2^(1//3)+(1)/(2(3)^(1//3)))^(10) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - Chapter 1
5 Videos
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - Chapter 2
7 Videos
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - chapter -3
1 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions
541 Videos
- LIMITSBOOK - CENGAGE PUBLICATIONCHAPTER - LIMITSEXERCISE - Comprehension Type
4 Videos
Similar Questions
For x∈R−{0,1}, let f1(x)=1x,f2(x)=1−xandf3(x)=11−x be three given functions. If a function, J(x) satisfies (f2oJof1)(x)=f3(x) then J(x) is equal to :
View Solutionlimy→0√1+√1+y4−√2y4
View SolutionThe equation of the plane passing through the point (1,1,1) and perpendicular to the planes 2x+y−2z=5and3x−6y−2z=7
View SolutionFind x satisfying [tanx]+[cotx]=2, where [.] represents the greatest integer function.
View Solutionlimx→0sin2xx
View SolutionThe last term in the binomial expansion of (213−1√2)n is (13.913)log38 then the 5th term from the beginning is
View SolutionIn (213+1313)n if the ratio of 7th term from the beginning to the 7th term from the end is 1/6, then find the value of n.
View SolutionIf the last tem in the binomial expansion of (213−1√2)nis(1353)log38 , then 5th term from the beginning is 210 b. 420 c. 105 d. none of these
View SolutionThe sum of the rational terms in the binomial expansion of (212+315)10 is :
View SolutionThe ratio of 11th term from the beginning and 11th term the end in the expansion of (2x−1x2)25 is −
View SolutionRatio of the 5th term from the beginning to the 5th term from the end in the binomial expansion of (21/3+12(3)1/3)10 is
View SolutionA ratio of the 5th term from the beginning and from the end in the binomial expansion of (21/3+12(3)1/3)10 is :
View SolutionLet x be the 7th term from the beginning and y be the 7th term from the end in the expansion of (31/3+141/3)n. If y=12x then the value of n is :
View SolutionIf the ratio of the 6th term from the beginning to the 6th term from the end in the expansion of (3√2+13√3)x is 16 then x=
View SolutionIn (33+133)n if the ratio of 7th term from the beginning to the 7th term from the end is 1/6, then find the value of n.
View Solution3th term from the end in expansion of (2+x)10 is
View Solution