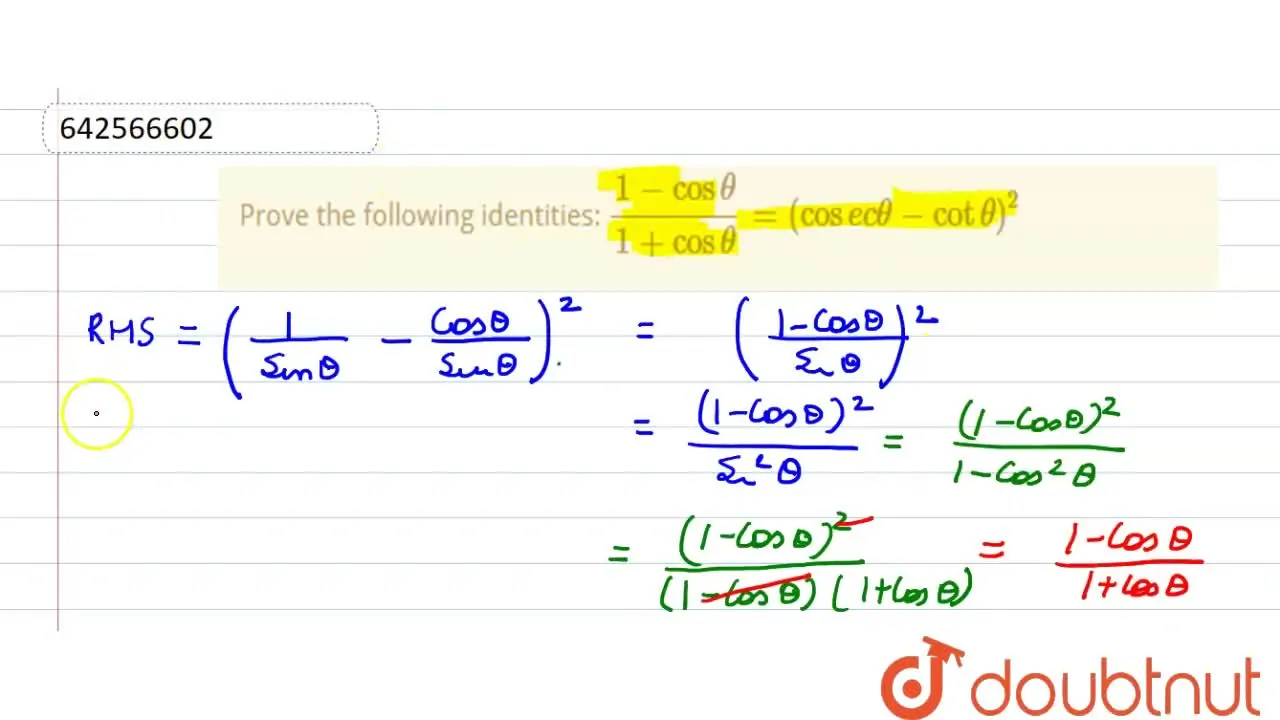
Prove the following identities: 1−cosθ1+cosθ=(cosecθ−cotθ)2
Step by step video & image solution for Prove the following identities: (1-costheta)/(1+costheta)=(cos e ctheta-cottheta)^2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
Similar Questions
Prove the following identities: (cosecθ−cotθ)2=1−cosθ1+cosθ
View SolutionProve the trigonometric identities: √1−cosθ1+cosθ=cosecθ−cotθ
View SolutionProve: sinθ1−cosθ=cosec θ+cotθ
View SolutionProve the following trigonometric identities: sinθ1−cosθ=cosecθ+cotθ
View SolutionProve the following identities: sinθcotθ+cosecθ=2+sinθcotθ−cosecθ
View SolutionProve that : 1−cosθ1+cosθ=(cotθ−cosecθ)2
View SolutionProve the following identities: cosθ1−sinθ+cosθ1+sinθ=2secθ
View SolutionProve the following identities: cosθ1−sinθ+cosθ1+sinθ=2secθ
View SolutionProve the following identities: (sinθ−secθ)2+(cosθ−cosecθ)2=(1−secθcosecθ)2
View SolutionProve the following identities: cos2θ1−tanθ+sin3θsinθ−cosθ=1+sinθcosθ
View Solution