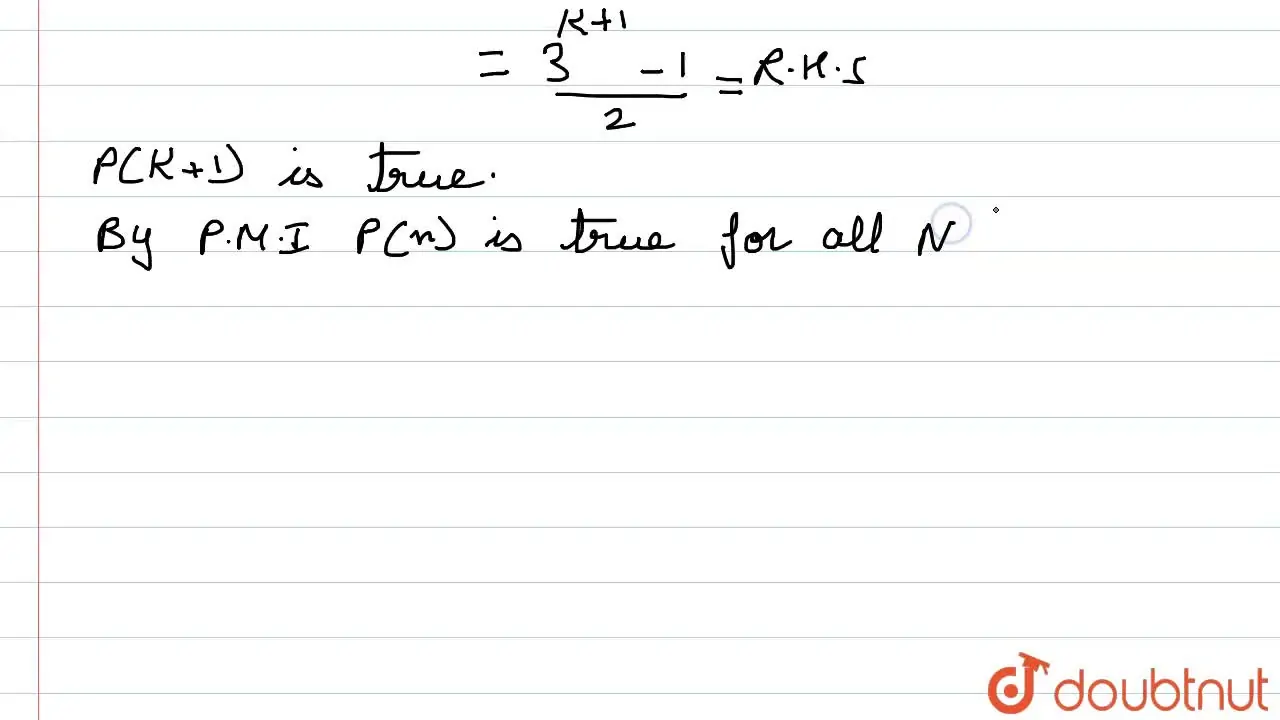Prove the following by using the principle of mathematical induction for all n∈N :- 1+3+32+....+3n−1=(3n−1)2. Solution in Punjabi
Step by step video & image solution for Prove the following by using the principle of mathematical induction for all n in N :- 1 +3 + 3^2 +....+3^(n-1)=((3^n-1))/2. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
Similar Questions
How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that repetition of the digits is allowed?
06:56View SolutionIn the following , describe the sample space for the indicated experiment. A coin is tossed three times.
03:47View SolutionProve the following by using the principle of mathematical induction for all n∈N:1+3+32+...+3n−1=(3n−1)2
03:19View SolutionProve the following by the principle of mathematical induction: 1+3+32++3n−1=3n−12
05:59View SolutionUsing the principle of mathematical induction, prove each of the following for all n∈N
1+2+3+4+…+N=12N(N+1).02:41View SolutionBy principle of mathematical induction,prove that 13+23+33+....+n3=[n(n+1)2]2for all n∈N
06:59View SolutionProve that by using the principle of mathematical induction for all n∈N:
1+3+32+….+3n−1=(3n−1)206:15View SolutionProve that by using the principle of mathematical induction for all n∈N:
1+3+32+….+3n−1=(3n−1)205:00View SolutionProve the following by using the principle of mathematical induction for all n∈N:1.2.3+2.3.4+...+n(n+1)(n+2)=n(n+1)(n+2)(n+3)4
10:23View SolutionProve the following by using the principle of mathematical induction for all n∈N:13+23+33+...........+n3=(n(n+1)2)2
05:52View SolutionUsing the principle of mathematical induction prove that : 1.3+2.32+3.33++n.3n=(2n−1)3n+1+34 for all n∈N .
03:51View SolutionUsing the principle of mathematical induction, prove that : 1.2.3+2.3.4++n(n+1)(n+2)=n(n+1)(n+2)(n+3)4 for all n∈N .
02:53View SolutionProve the following by using the principle of mathematical induction for all n∈N : 13+23+33+...+n3=(n(n+1)2)2
08:17View SolutionProve the following by the principle of mathematical induction: 1+3+32++3n−1=3n−12
07:29View SolutionProve the following by the principle of mathematical induction: 1.2+2.3+3.4++n(n+1)=n(n+1)(n+2)3
03:34View SolutionProve the following by using the principle of mathematical induction for all n∈N
13+23+33+…………….+n3=(n(n+1)2)207:17View Solution