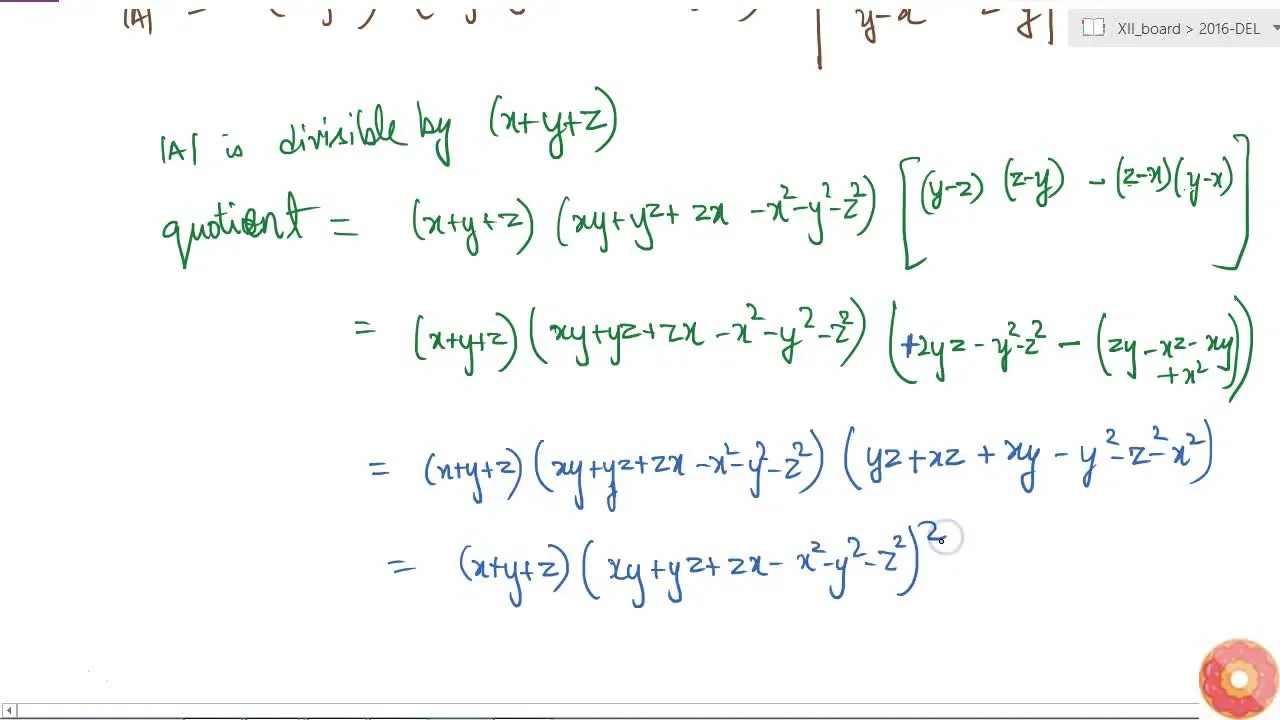Prove that ∣∣ ∣ ∣∣yz−x2zx−y2xy−z2zx−y2xy−z2yz−x2xy−z2yz−x2zx−y2∣∣ ∣ ∣∣ is divisible by (x+y+z), and hence find the quotient.
Δ=∣∣
∣
∣∣yz−x2zx−y2xy−z2zx−y2xy−z2yz−x2xy−z2yz−x2zx−y2∣∣
∣
∣∣
Applying C1→C1+C2+C3
Δ=∣∣
∣
∣∣xy+yz+zx−x2−y2−z2zx−y2xy−z2xy+yz+zx−x2−y2−z2xy−z2yz−x2xy+yz+zx−x2−y2−z2yz−x2zx−y2∣∣
∣
∣∣
=(xy+yz+zx−x2−y2−z2)∣∣
∣
∣∣1zx−y2xy−z21xy−z2yz−x21yz−x2zx−y2∣∣
∣
∣∣
Now, applying R1→R1−R3 and R2→R2−R3
=(xy+yz+zx−x2−y2−z2)∣∣
∣
∣∣0zx−y2−yz+x2xy−z2−zx+y20xy−z2−yz+x2yz−x2−zx+y21yz−x2zx−y2∣∣
∣
∣∣
=(xy+yz+zx−x2−y2−z2)∣∣
∣
∣∣0(x−y)(x+y+z)(y−z)(x+y+z)0(x−z)(x+y+z)(y−x)(x+y+z)1yz−x2zx−y2∣∣
∣
∣∣
=(xy+yz+zx−x2−y2−z2)(x+y+z)2∣∣
∣
∣∣0(x−y)(y−z)0(x−z)(y−x)1yz−x2zx−y2∣∣
∣
∣∣
=(xy+yz+zx−x2−y2−z2)(x+y+z)2[(x−y)(y−x)−(x−z)(y−z)]
=(xy+yz+zx−x2−y2−z2)(x+y+z)2[xy+yz+zx−x2−y2−z2]
Δ=(xy+yz+zx−x2−y2−z2)2(x+y+z)2
∴Δ is divisible by (x+y+z) and quotient is (xy+yz+zx−x2−y2−z2)2(x+y+z).
Related Playlists
Similar Questions
Prove that ∣∣ ∣ ∣∣yz−x2zx−y2xy−z2zx−y2xy−z2yz−x2xy−z2yz−x2zx−y2∣∣ ∣ ∣∣ is divisible by (x+y+z), and hence find the quotient.
View SolutionProve that det⎛⎜⎝yx−x2zx−y2xy−z2zx−y2xy−z2yz−x2xy−z2yz−x2zx−y2⎞⎟⎠ is divisible by (x+y+z) and hence find the quotient.
View SolutionShow that ∣∣ ∣ ∣∣yz−x2zx−y2xy−y2zx−y2xy−z2yz−x2xy−z2yz−x2zx−y2∣∣ ∣ ∣∣=∣∣ ∣ ∣∣r2u2u2u2r2u2u2u2r2∣∣ ∣ ∣∣ where r2=x2+y2+z2 and u2=xy+yz+zx
View SolutionProve that ∣∣ ∣ ∣∣x2x2−(y−z)2yzy2y2−(z−x)2zxz2z2−(x−y)2xy∣∣ ∣ ∣∣
=(x−y)(y−z)(z−x)(x+y+z)(x2+y2+z2)View Solution∣∣ ∣ ∣∣x2y2+z2yzy2z2+x2zxz2x2+y2xy∣∣ ∣ ∣∣ is divisible by
View Solution∣∣ ∣ ∣∣1x1y1zx2y2z2yzzxxy∣∣ ∣ ∣∣
View SolutionProve that ∣∣ ∣ ∣∣xyzx2y2z2yzzxxy∣∣ ∣ ∣∣=∣∣ ∣ ∣∣111x2y2z2x3y3z3∣∣ ∣ ∣∣
View Solution(x−y−z)2−(x2+y2+z2)=2(yz−zx−xy)
View Solutionprove that:∣∣ ∣ ∣∣y2z2yzy+zz2x2zxz+xx2y2xyx+y∣∣ ∣ ∣∣=0
View Solutionfactorise: ∣∣ ∣ ∣∣xyzx2y2z2yzzxxy∣∣ ∣ ∣∣
View Solution