Prove that the perimeter of a right-angled triangle of given hypotenuse is maximum when the triangle is isosceles
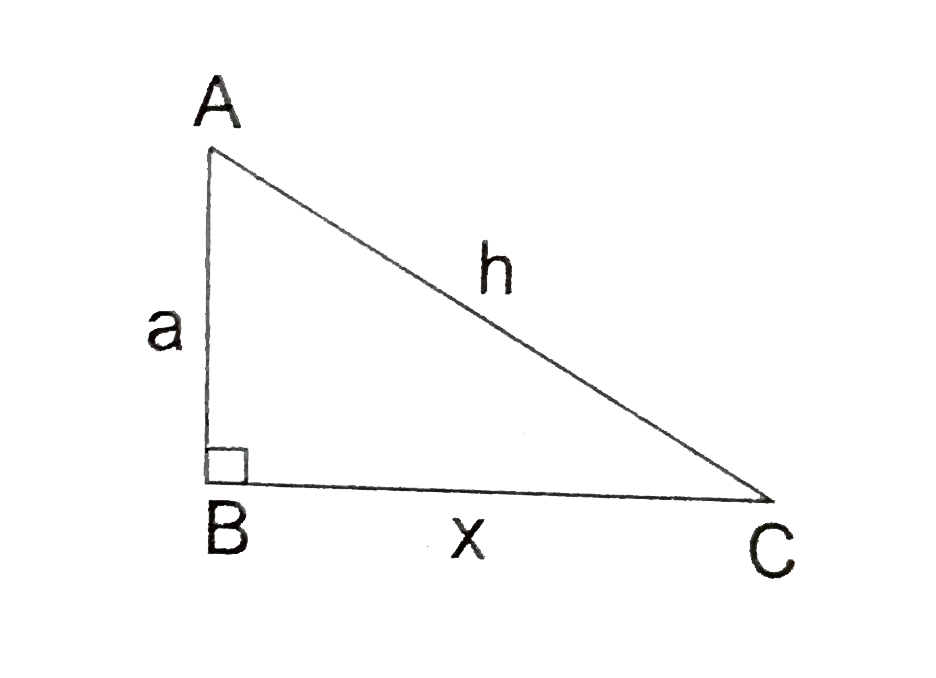
Let ABC be the right triangle with given hypotenuse h
Let, base BC = x and altitude BA=a
Then, h2=x2+a2⇒a=√h2−x2
∴P=a+x+h⇒P=√(h2−x2)+x+h
So, dPdx=−x√h2−x2+1andd2Pdx2=−h2(h2−x2)3/2
Now, dPdx=0⇒x=h√2
And for x=h√2,d2Pdx2=−23/2h<0
∴ P is maximum when x=h√2anda=h√2 i.e., when x = a
Related Playlists
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11G32videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11H30videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11E22videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - ADJOINT AND INVERSE OF A MATRIXEXERCISE - Exercise 737videos
ADJOINT AND INVERSE OF A MATRIX
- BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 1739videos
AREA OF BOUNDED REGIONS
Similar Questions
Prove that the area of right-angled triangle of given hypotenuse is maximum when the triangle is isosceles.
View SolutionProve that the perimeter of a right - angled triangle of given hypotenuse equal to 5 cm is maximum when the triangle is isosceles.
View SolutionThe maximum area of a right angled triangle with hypotenuse h is
View SolutionThe maximum area of a right angled triangle with hypotenuse h is :
View SolutionThe perimeter of a right angled triangle is 24 cm. If its hypotenuse is 10 cm then area of this triangle is
View SolutionThe perimeter of a right angled triangle is 12 cm . The hypotenuse is 5 cm , then the area of the triangle is
View SolutionThe perimeter of a right angled triangle is 60 cm. Its hypotenuse is 26 cm. The area of the triangle is
View SolutionThe perimeter of a right angled triangle is 12 cm . The hypotenuse is 5 cm , then the area of the triangle is
View SolutionThe perimeter of a right angled triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
View SolutionThe perimeter of an isosceles right triangle is 2p, its area is
View Solution


