सिद्ध कीजिए कि समद्विबाहु त्रिभुज के आधार की माध्यिका उस पर लम्ब होता है |
दिया है - समद्विबाहु ΔABC , जिसमे AB = BC तथा आधार BC का मध्य बिन्दु D है | |
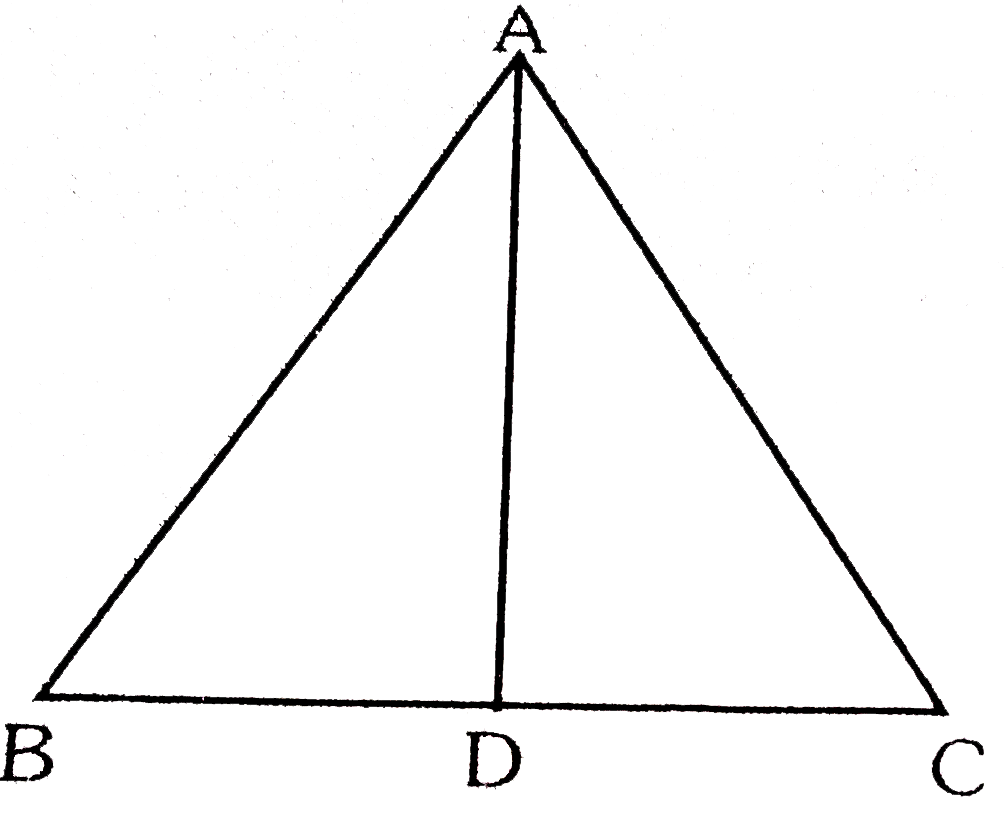
सिद्ध करना है -
AD⊥BC
माना ∣∣→b∣∣=AB तथा |→c|=AC
∴→AD=→b+→c2
तथा −−→BC=−−→BA+−−→AC=−−→AC−−−→AB=→c−→b
अब −−→AC=−−→BC=12(→b+→c)−(→c−→b)=12(→c+→b)(→c−→b)
=12[(c)2−(b)2]12[AC2−AB2]
=12(AB2−AB2)=0(∵−−→AB=−−→AB)
अतः −−→AD तथा−−→BC परस्पर लम्ब सदिश है |
Related Playlists
- BOOK - BALAJI PUBLICATIONCHAPTER - सदिश राशियों का गुणनफल EXERCISE - विविध उदाहरण21videos
सदिश राशियों का गुणनफल
- BOOK - BALAJI PUBLICATIONCHAPTER - सदिश राशियों का गुणनफल EXERCISE - अभ्यस प्रश्न 20.116videos
सदिश राशियों का गुणनफल
- BOOK - BALAJI PUBLICATIONCHAPTER - सदिश बीजगणित EXERCISE - स्वमूल्यांकन परीक्षण23videos
सदिश बीजगणित
- BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन EXERCISE - स्वमूल्यांकन परीक्षण24videos
समाकलन
Similar Questions
सिद्ध कीजिए की निम्नलिखित सदिश परस्पर लम्ब है -
→a=ˆi+2ˆj+ˆk,→b=ˆi+ˆj−3ˆk,→c=7ˆi−4ˆj+ˆk07:05View Solutionसदिशों का अदिश गुणनफल ज्ञात कीजिए -
3ˆi+8ˆj−2ˆkव्5ˆi+ˆj+2ˆk05:40View Solutionसदिश →a=ˆi−2ˆj+ˆk,→b=−2ˆi+4ˆj+5ˆk और →c=ˆi−6ˆj−7ˆk का योगफल ज्ञात कीजिए।
01:47View Solutionमान ज्ञात कीजिए -∫(4e3x+1)dx
03:54View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
03:21View Solutionसिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है यदि
∣∣ ∣ ∣∣1111+cosA1+cosB1+cosCcos2A+cosAcos2B+cosBcos2C+cosC∣∣ ∣ ∣∣=004:17View Solutionकथन सत्य है या असत्य
त्रिभुज कि भुजाओ के लम्ब समद्विभाजक संगामी होते है।04:36View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
02:50View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
04:56View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
06:04View Solutionसिद्ध कीजिए कि किसी समचतुष्फलक कि कोई दो सम्मुख कोरें परस्पर लम्ब होती हैं |
46:34View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
03:43View Solutionपरवलय y2=4px की किसी द्विकोटि की लम्बाई 8p है। सिद्ध कीजिए कि शीर्ष को उसके सिरों से मिलाने वाली सरल रेखाएँ परस्पर लम्ब है।
04:14View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
View Solutionत्रिभुज के आधार पर कुछ महत्वपूर्ण प्रश्न
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solution


