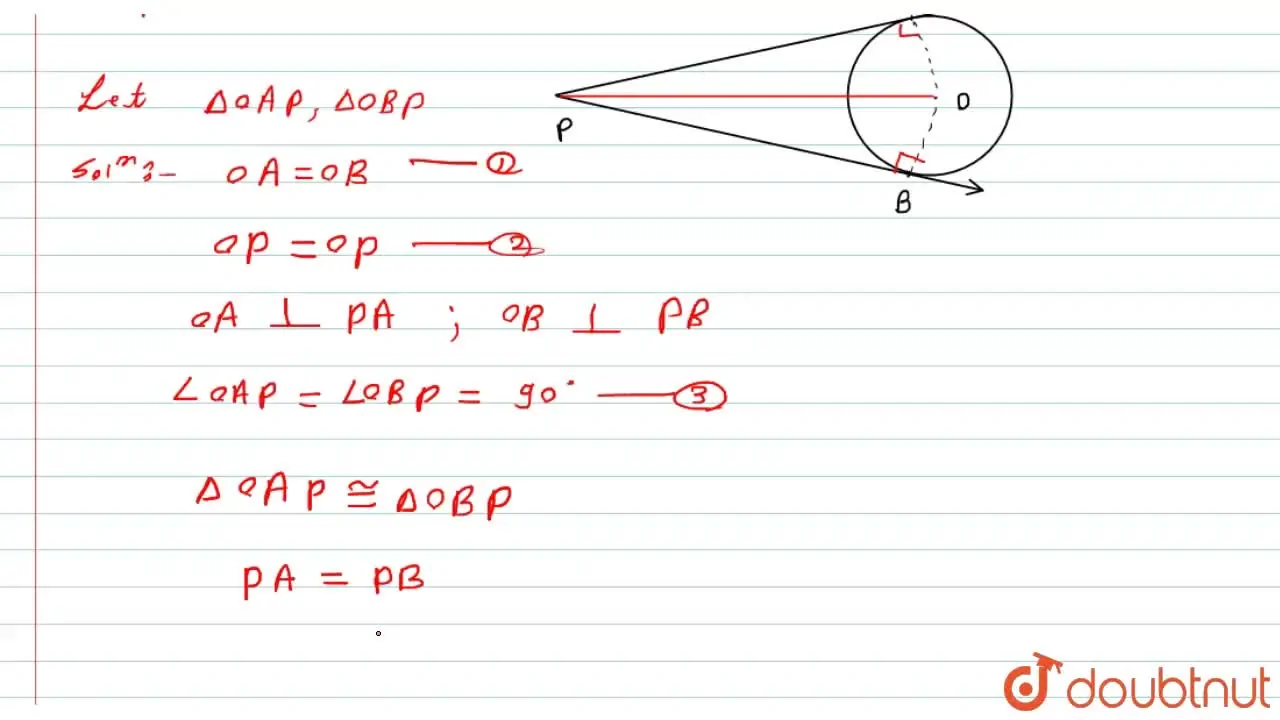
Prove that the length of the tangents drawn from an external point to a circle are equal.
Step by step video & image solution for Prove that the length of the tangents drawn from an external point to a circle are equal. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
Similar Questions
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
View SolutionProve that the angle between two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the centre.
View SolutionABCD is a quadrilateral in which a circle is inscribed.
Statement:1 The length of the sides of the quadrilateral can be A.P.
and Statement: 2: The length of tangents from an external point to a circle are equal.View SolutionProve that The length of tangent from an external point on a circle is always greater than the radius of the circle.
View SolutionProve that the tangent lines drawn from the outer point to the circle are equal? Or
View SolutionStatement-1: The line x+9y−12=0 is the chord of contact of tangents drawn from a point P to the circle 2x2+2y2−3x+5y−7=0.
Statement-2: The line segment joining the points of contacts of the tangents drawn from an external point P to a circle is the chord of contact of tangents drawn from P with respect to the given circleView SolutionFind the equation to the chord of contact of the tangents drawn from an external point (−3,2) to the circle x2+y2+2x−3=0.
View SolutionFind the equation to the chord of contact of the tangents drawn from an external point (−3,2) to the circle x2+y2+2x−3=0.
View SolutionIf the angle between two tangents drawn from an external point P to a circle of radius 'a' and centre O, is 60∘, then find the length of OP.
View SolutionIf the angle between two tangents drawn from an external point ‘P’ to a circle of radius ‘r’ and centre O is 60∘, then find the length of OP.
View Solution