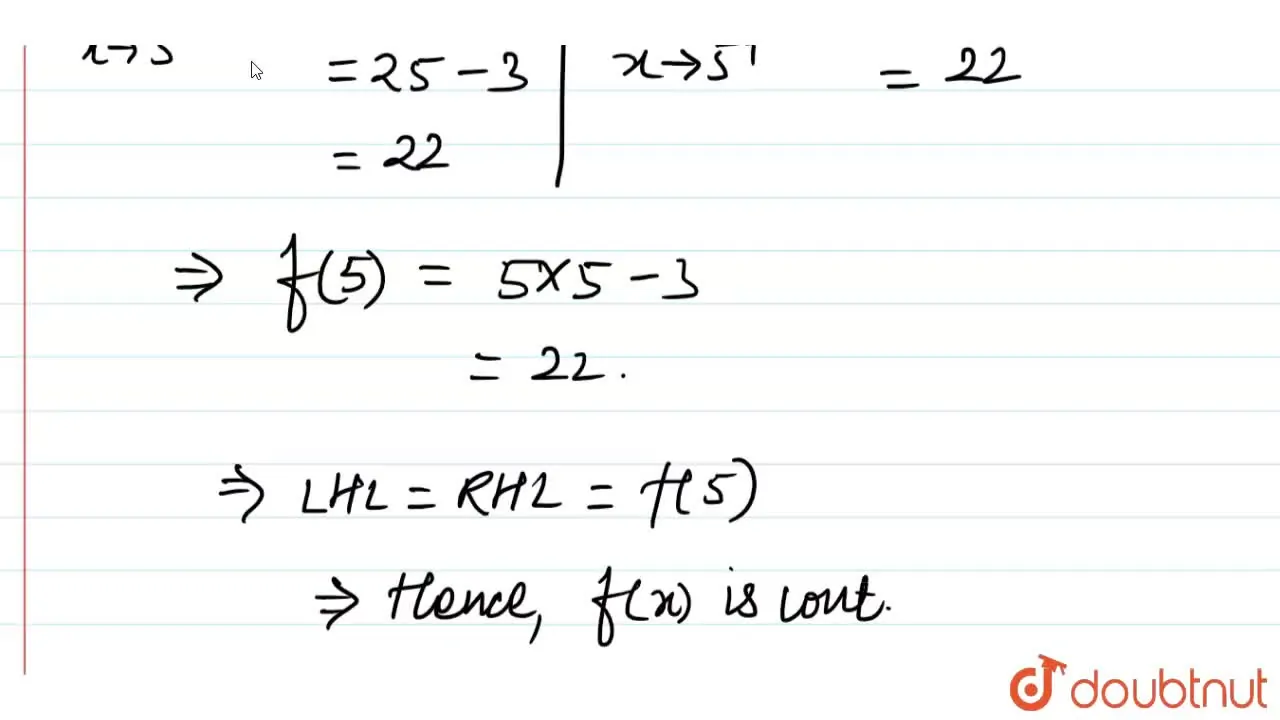Prove that the function f(x)=5x−3is continuous at x=0, at x=−3and at x=5.
The given function is f(x)=5x−3
At x=0,f(0)=5(0)−3=−3
limx→3f(x)=limx→3f(5x−3)=5(0)−3=−3
∴limx→3f(x)=f(0)
Therefore, f is continous at x=0
At x=−3,f(−3)=5(−3)−3=−18
limx→−3f(x)=limx→−3(5x−3)=5(−3)−3=−18
∴limx→−3f(x)=f(−3)
Therefore , f is continuous at x=-3
At x=5,f(x)=f(5)=5(5)−3=25−3=22
limx→5f(x)=limx→5(5x−3)=5(5)−3=22
limx→5f(x)=f(5)
Therefore, f is continuous at x=5.
Hence f is continuous at all the given points (In fact f is continous for all R, Since it is a polynomial)
Related Playlists
- BOOK - NCERT ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 5.410videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - NCERT ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 5.315videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - NCERT ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 5.210videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - NCERT ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - EXERCISE 8.27videos
APPLICATION OF INTEGRALS
- BOOK - NCERT ENGLISHCHAPTER - DETERMINANTSEXERCISE - All Questions116videos
DETERMINANTS
Similar Questions
Show that the function f(x)=2x−|x| is continuous at x=0.
View SolutionShow that the function f(x)=2x−|x| is continuous at x=0 .
View SolutionProve that the function f(x)=2x2−3x+2 is continuous at at x=1.
View SolutionFind the values of a and b so that the function f given by f(x)={1, if x<=3, ax+b , if 3 < x < 5, 7 if x >= 5 is continuous at x=3 and x=5 .
View SolutionFind the values of a and b so that the function f given by f(x)={ax+b, if 3 < x<5, 1 if x<=3, 7 if x > = 5 is continuous at x=3andx=5.
View SolutionProve that the function defined by f(x)=tanxis a continuous function.
View SolutionExamine whether the function f given by f(x)=x3 is continuous at x=0
View SolutionIf the function f(x)=sin10xx , x≠0 is continuous at x=0 , find f(0) .
View SolutionProve that f(x)=√|x|−x is continuous for all x≥0 .
View SolutionProve that f(x)=√|x|−x is continuous for all x≥0.
View Solution