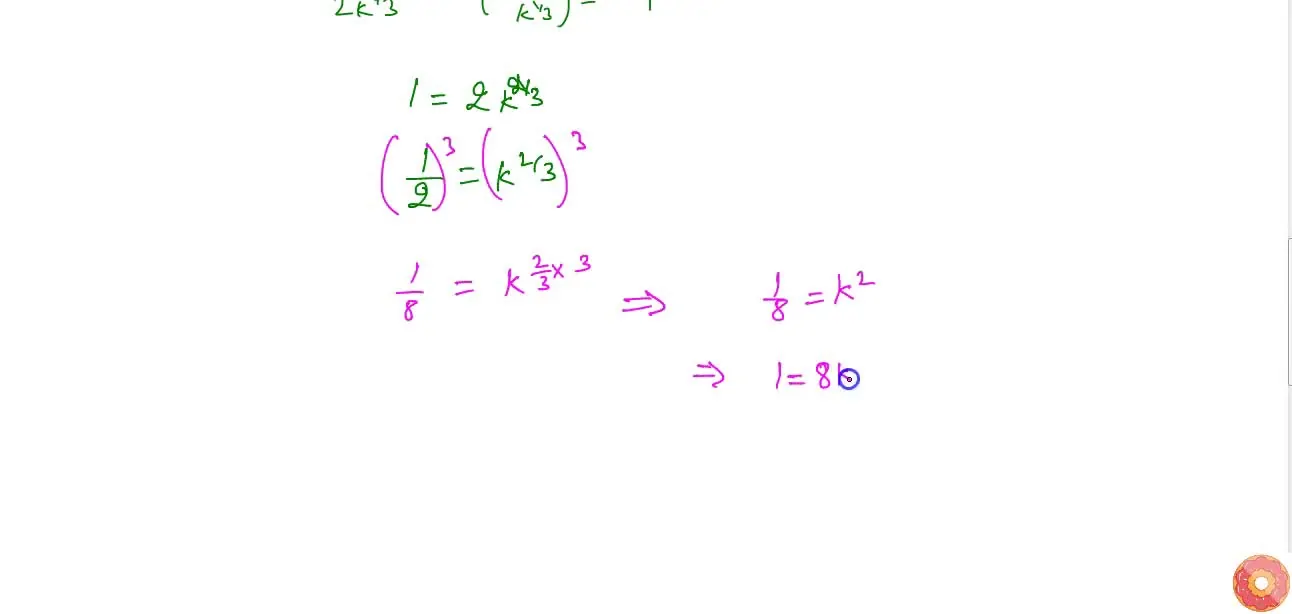Prove that the curves x=y2 and x y=k intersect at right angles if 8k2=1.
Video Solution
Text Solution
x=y2
xy=k
y3=k
y=k3
x=h23
Point of intersection(k23,k13)
Slope of tangent at(k23,k13)onx=y2
for curve xy=k
y=kx⇒dydx=−kx2
slope of tangent AT(K23,K13) ON XY=K
(slope of T1)*(slope of T2)=-1
12k13⋅(−1k13)=−1
1=2k13
(12)3=(k23)3
18=k23⋅3
1=8k2
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Prove that the curves x=y2 and x y=k intersect at right angles if 8k2=1.
View SolutionProve that the curves x=y2and xy=k cut at right angles* if 8k2=1.
View SolutionShow that the curves 2x=y2 and 2xy=k cut each other at right angles if k2=8
View SolutionShow that the curves 4x=y2 and 4xy=k cut at right angles, if k2=512 .
View SolutionShow that the curves 2x=y2 and 2xy=k cut at right angles, if k2=8 .
View SolutionShow that the curves x=y2 and xy=k cut at right angles, if 8k2=1 .
View SolutionShow that the curves 2x=y2and2xy=k cut at right angles, if k2=8.
View SolutionProve that the curve y=x2 and xy=k intersect orthogonally if 8k2=1.
View SolutionShow that the curves x=y2 and xy=k cut at right angles; if 8k2=1
View SolutionShow that the curves x=y2andxy=k cut at right angles, if 8k2=1
View Solution