Prove that ∑1≤i<∑j≤n(i)=n(n2−1)6
To prove that
n∑i=1n∑j=i+1i=n(n2−1)6,
we will follow a systematic approach.
Step 1: Understanding the Summation
We need to evaluate the double summation n∑i=1n∑j=i+1i. Here, i ranges from 1 to n, and for each fixed i, j ranges from i+1 to n.
Step 2: Rewriting the Inner Summation
For a fixed i, the inner summation n∑j=i+1i counts i a number of times equal to the number of valid j values. The number of j values is n−i (since j can take values from i+1 to n). Thus, we can rewrite the inner summation as:
n∑j=i+1i=i(n−i).
Step 3: Substituting Back into the Outer Summation
Now substituting back into the outer summation, we have:
n∑i=1n∑j=i+1i=n∑i=1i(n−i).
Step 4: Expanding the Summation
We can expand this summation:
n∑i=1i(n−i)=nn∑i=1i−n∑i=1i2.
Step 5: Using Known Formulas
We can use the formulas for the summation of the first n natural numbers and the sum of squares:
1. n∑i=1i=n(n+1)2
2. n∑i=1i2=n(n+1)(2n+1)6
Substituting these into our expression gives:
n⋅n(n+1)2−n(n+1)(2n+1)6.
Step 6: Finding a Common Denominator
To combine these two fractions, we need a common denominator. The common denominator for 2 and 6 is 6. Thus, we rewrite:
n⋅n(n+1)2=3n(n(n+1))6=3n2(n+1)6.
Now we can combine:
3n2(n+1)−n(n+1)(2n+1)6.
Step 7: Simplifying the Numerator
Now, simplifying the numerator:
3n2(n+1)−n(n+1)(2n+1)=n(n+1)(3n−(2n+1))=n(n+1)(n−1).
Step 8: Final Expression
Thus, we have:
n∑i=1n∑j=i+1i=n(n+1)(n−1)6.
Since n(n+1)(n−1)=n(n2−1), we can conclude:
n∑i=1n∑j=i+1i=n(n2−1)6.
Conclusion
This proves that
n∑i=1n∑j=i+1i=n(n2−1)6.
We need to evaluate the double summation n∑i=1n∑j=i+1i. Here, i ranges from 1 to n, and for each fixed i, j ranges from i+1 to n.
For a fixed i, the inner summation n∑j=i+1i counts i a number of times equal to the number of valid j values. The number of j values is n−i (since j can take values from i+1 to n). Thus, we can rewrite the inner summation as:
Now substituting back into the outer summation, we have:
We can expand this summation:
We can use the formulas for the summation of the first n natural numbers and the sum of squares:
2. n∑i=1i2=n(n+1)(2n+1)6
To combine these two fractions, we need a common denominator. The common denominator for 2 and 6 is 6. Thus, we rewrite:
Now, simplifying the numerator:
Thus, we have:
This proves that
Similar Questions
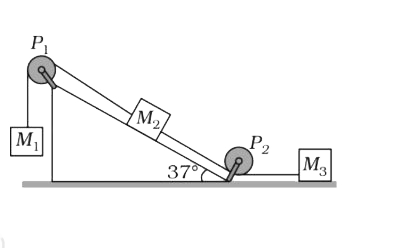
Masses M1,M2 and M3 are connected by strings of negligible mass which pass over massless and frictionless pulleys P1 and P2 as shown in the figure. The masses move such that the portion of the string betweenP1 and P2 is parallel to the inclined plane and the portion of the string between P2 and M3 is horizontal. The masses M2 and M3 are 4.0 kg each and the coefficient of kinetic friction between both the masses and the surfaces is 0.25. The inclined plane makes an angle of 37° with the horizontal. If the mass M1 moves downwards with a uniform velocity, find
(i) the mass of M1 in kg
(ii) the tension in the horizontal portion of the string in Newton
 View Solution
View SolutionIf ai>0 (i=1,2,3,….n) prove that
∑1≤i≤j≤n√aiaj≤n−12(a1+a2+….+an)View SolutionProve that s∑r=0n∑s=1^nCnsCr=3n−1.
View Solution∞∑n=12nn!=
View SolutionIf (1+x)n=n∑r=0Cr,xr, then prove that
(∑∑)0≤i<j≤n(iCi+jCj)=n22n∑r=01Cr .View SolutionProve that n∑r=0r2.Cr=n(n+1).2n−2
View SolutionProve that n∑r=1r3(nC_rCr−1)2=n(n+1)2(n+2)12
View SolutionProve that n∑k=0(−1)k.3nCk=(−1)n.3n−1Cn
View Solution∞∑n=12n2+n+1(n!) =
View Solution∞∑n=11(2n−1)!=
View Solution
