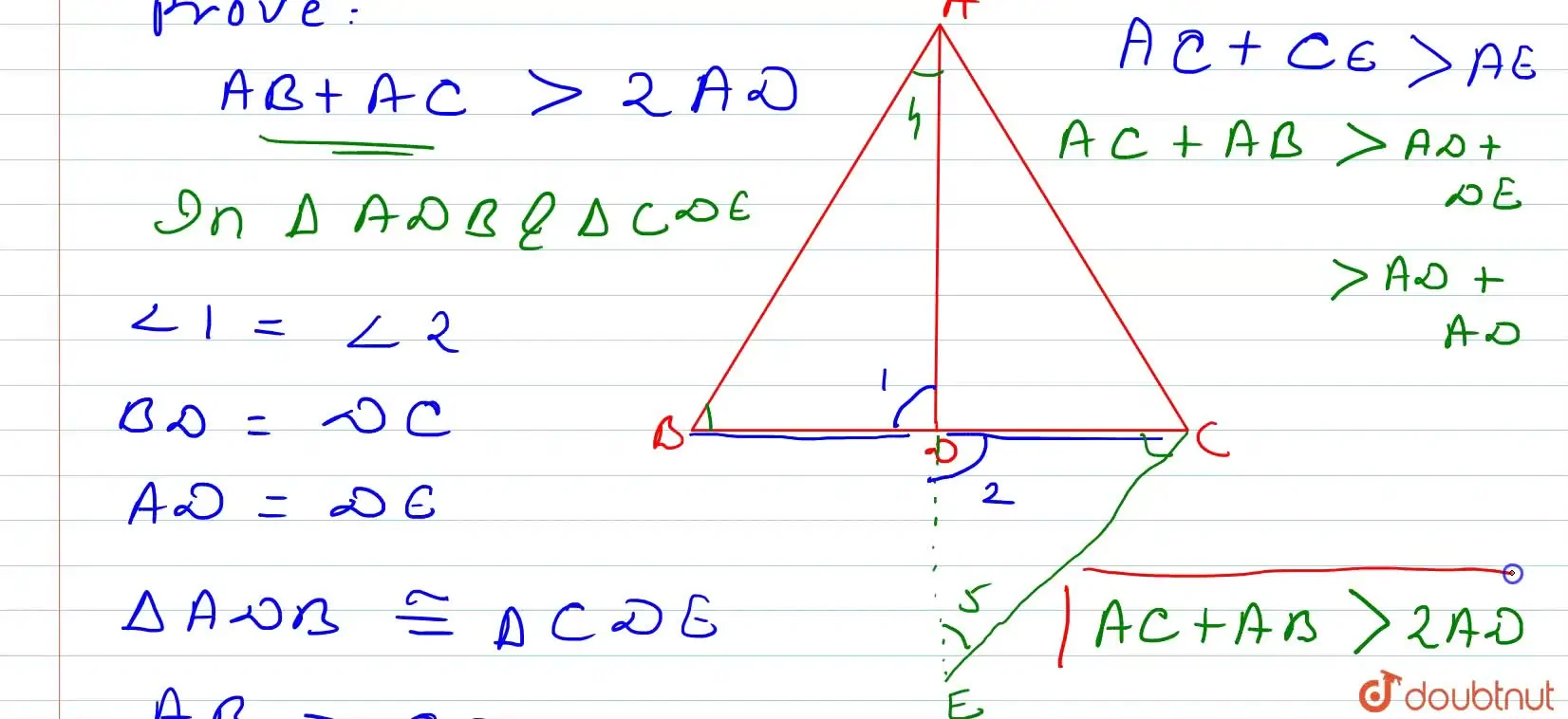
Prove that sum of any two sides of a triangle is greater than twice the median with respect to the third side.
Given : ΔABC with median AD.
To prove : AB+AC>2AD
Construction : Produce AD to E such that DE=AD and join EC.
Proof : In ΔADB and ΔEDC.
∵⎧⎪⎨⎪⎩AD=ED(by construction)∠1=∠2(vertically opposite angles)DB=DC(given)
∴ΔADB≅ΔEDC (By SAS criterion)
∴AB=EC (c.p.c.t.)
and ∠3=∠4 (c.p.c.t)
Now, in ΔAEC, we have
AC+CE>AE (∵ sum of any sides of a triangle is greater than the third side)
⇒ AC+CE>AD+DE
⇒ AC+CE>AD+AD (∵AD=DE)
⇒ AC+CE>2AD
⇒ AC+AB>2AD (∵AB=EC)

Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar5videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7a35videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)10videos
SURFACE AREA AND VOLUME
Similar Questions
Prove that sum of any two sides of a triagle is greater than twice the median with respect to the third side.
View SolutionProve that sum of any two medians of a triangle is greater than the third median.
View SolutionSum of any two sides of a triangle is greater than the third side.
View SolutionThe sum of any two sides of a triangle is greater than third side.
View SolutionProve that the sum of any two sides of a triangle is greater than two times the median of third side.
View SolutionProperty The sum of any two sides of a triangle is greater than the third side.
View SolutionWhich of the following statements are true (T) and which are false (F)? Sum of the three sides of a triangle is less than the sum of its three altitudes. Sum of any two sides of a triangle is greater than twice the median drawn to the third side. Sum of any two sides of a triangle is greater than the third side. Difference of any two sides of a triangle is equal to the third side. If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it. Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
View SolutionProve that any two sides of a triangle are together greater than twice the median drawn to the third side. GIVEN : ABC in which AD is a median. PROVE : AB+AC>2AD CONSTRUCTION : Produce AD to E such that AD=DE. Join EC.
View SolutionProve that any two sides of a triangle are together greater than twice the median drawn to the third side.
View SolutionSum of any two sides of a triangle is not less than the third side
View Solution