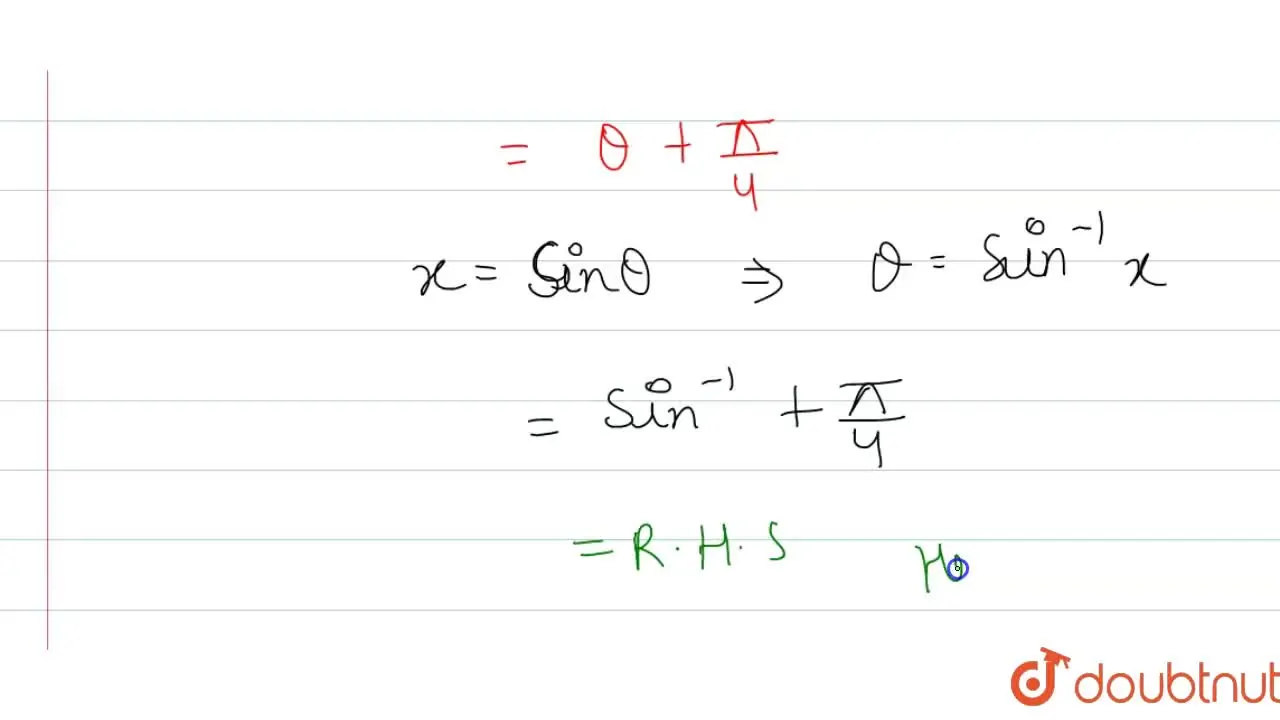Prove that sin−1.((x+√1−x2√2)=sin−1x+π4, where −1√2<x<1√2
Video Solution
Text Solution
The correct Answer is:sin−1x+π4
Let x=sinθ, where
−1√2<x<1√2
⇒−π4<θ<π4
sin−1(x+√1−x2√2)=sin.−1(sinθ+cosθ√2)
=sin.−1(sin(θ+π4))
=θ+π4(∵θ+π4∈(0,π2))
=sin−1x+π4
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.26videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.312videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Question Bank24videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - JEE Previous Year20videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
Similar Questions
Prove that sin−1x+sin−1√1−x2=π2
View Solutiony=sin−1(2x√1−x2),−1√2<x<1√2
View SolutionProve that sin−1(2x√1−x2)=2cos−1x,1√2≤x≤1
View SolutionProve that :
sin−1(2x√1−x2)=2sin−1x,−1√2≤x≤1√2View SolutionProve that :
sin−1(2x√1−x2)=2sin−1x,−1√2≤x≤1√2View SolutionProve that: sin−1{√1+x+√1−x2}=π4+sin−1x2,0<x<1
View SolutionProve that sin−1{√1+x+√1−x2}=π4+cos−1x2,0<x<1
View SolutionProve that cos−1{√1+x2}=cos−1x2,−1<x<1
View SolutionProve that tan−1{xa+√a2−x2}=12sin−1.xa,−a<x<a
View SolutionProve that sin[2tan−1{√1−x1+x}]=√1−x2
View Solution