Prove that
(i)1−sinθ1+sinθ=(secθ−tanθ)2
(ii)(1+cosθ)(1−cosθ)=(cosecθ+cotθ)2
We have
(i)RHS=(secθ−tanθ)2
=(1cosθ−sinθcosθ)2=(1−sinθcosθ)2=(1−sinθ)2cos2θ
=(1−sinθ)2(1−sin2θ)=(1−sinθ)(1−sinθ)(1+sinθ)(1−sinθ)
=(1−sinθ)(1+sinθ)=LHS.
∴RHS=LHS.
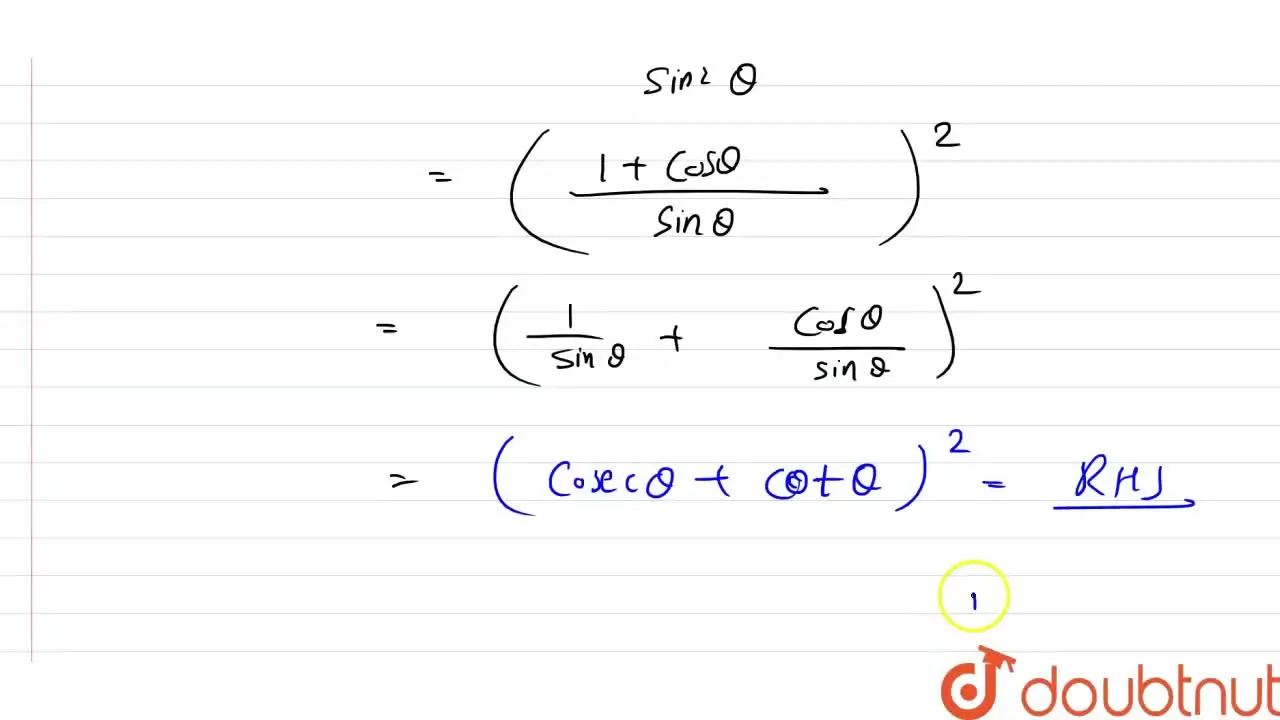
(ii)RHS=(cosecθ+cotθ)2=(1sinθ+cosθsinθ)2
=(1+cosθsinθ)2=(1+cosθ)2sin2θ=(1+cosθ)(1+cosθ)1−cos2θ
=(1+cosθ)(1+cosθ)(1+cosθ)(1−cosθ)=(1+cosθ)(1−cosθ)=LHS.
∴LHS=RHS.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Exercise 13A38videos
TRIGONOMETRIC IDENTITIES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Exercise 13B15videos
TRIGONOMETRIC IDENTITIES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Test Yourself20videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOSEXERCISE - Exercise 1035videos
TRIGONOMETRIC RATIOS
Similar Questions
Prove each of the following identities :
(i)√1+sinθ1−sinθ=(secθ+tanθ)
(ii)√1−cosθ1+cosθ=(cosecθ−cotθ)
(iii)√1+cosθ1−cosθ+√1−cosθ1+cosθ=2cosecθView SolutionProve the following trigonometric identities: √1−sinθ1+sinθ=secθ−tanθ √1+cosθ1−cosθ=cosecθ+cotθ
View SolutionProve that: 1+sinθ−cosθ1+sinθ+cosθ=tanθ2
View SolutionProve that 1+sinθ−cosθ1+sinθ+cosθ=tan(θ2)
View SolutionProve that
(i)sinθ(1−cosθ)=(cosecθ+cotθ)
(ii)1(secθ−tanθ)=(secθ+tanθ)View SolutionProve that cosθ1+sinθ=1−sinθcosθ=secθ−tanθ
View SolutionProve that
(secθ+tanθ)(1−sinθ)=cosθView SolutionProve each of the following identities :
(i)secθ(1−sinθ)(secθ+tanθ)=1
(ii)sinθ(1+tanθ)+cosθ(1+cotθ)=(secθ+cosecθ)View SolutionProve that cosθ−sinθ+1cosθ+sinθ−1=cosecθ+cotθ
View SolutionProve that: sinθ1−cosθ+tanθ1+cosθ=cosecθ+cotθ+secθcosecθ−cosecθ
View Solution