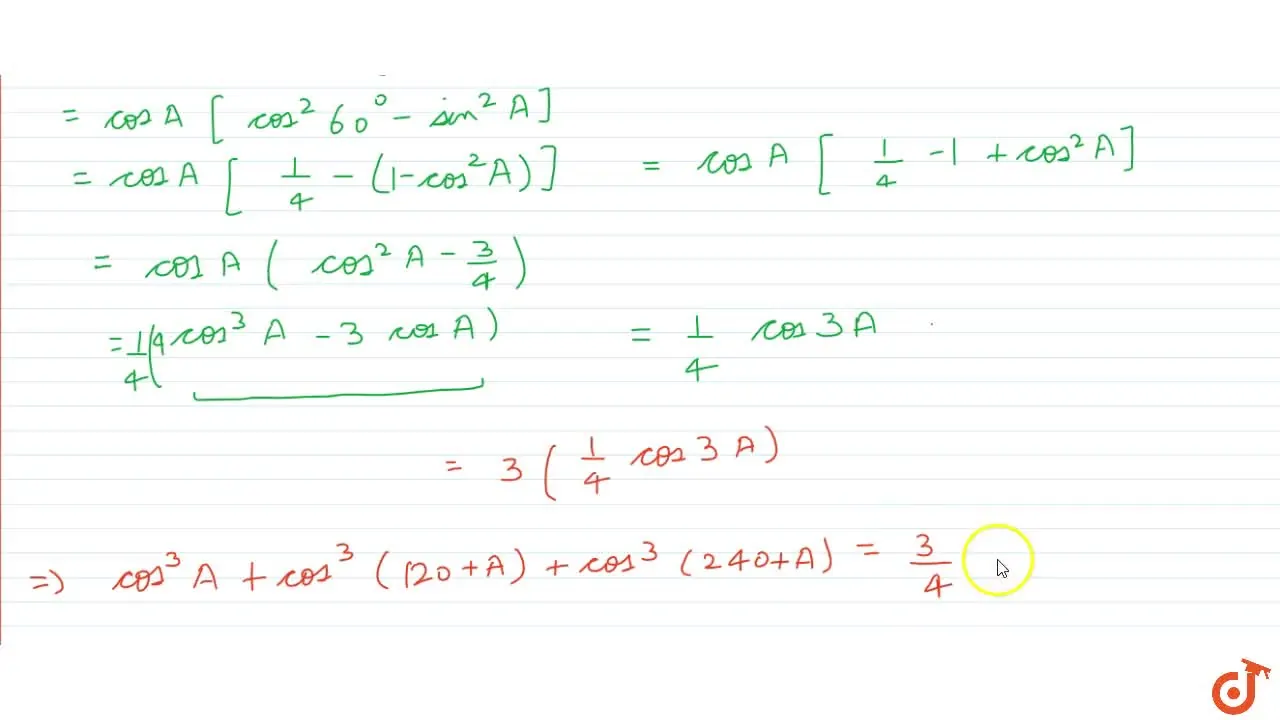Prove that cos3A+cos3(1200+A)+cos3(2400+A)=34cos3A
Video Solution
Text Solution
cosA+cos(120∘+A)+cos(240∘+A)
=cosA+(2cos(120+A+240+A2)cos(120+A−240−A2))
=cosA+(2cos(180+A)cos(−60∘))
=cosA+(2cos(180+A)cos60∘)
=cosA+(−2cosA(12))
=cosA−cosA=0
We know, when, a+b+c=0,
a3+b3+c3=3abc
∴L.H.S.=cos3A+cos3(120∘+A)+cos3(240∘+A)=3cosAcos(120∘+A)cos(240∘+A)
=3cosAcos(180−(60−A))cos(180+(60+A))
=3cosAcos(−(60−A))cos(−(60+A))
=3cosAcos(60−A)cos(60+A)
Using cos(C−D)cos(C+D)=cos2C−sin2D
=3cosA[cos260∘−sin2A]
=3cosA[14−(1−cos2A)]
=3cosA[−34+cos2A]
=34(4cos3A−3cosA)
=34cos3A=R.H.S.
|
Updated on:21/07/2023
Related Playlists
Similar Questions
cos3A+cos3(120+A)+cos3(240+A)=34Cos3A
View SolutionProve that cos3A+cos3(1200+A)+cos3(2400+A)=34cos3A
View SolutionProve that: cosAcos(600−A)cos(600+A)=14cos3A
View SolutionProve that cos(120∘−A)+cosA+cos(120∘+A)=0.
View SolutionProve that :cosAcos(60−A)cos(60+A)=14cos3A
View SolutionProve that:
(i) cosAcos(60∘−A)cos(60∘+A)=14cos3A
(ii) tanA+tan(60∘+A)−tan(60∘−A)=3tan3A.View SolutionProve that : cos3Acos3A+sin3Asin3A=cos32A
View SolutionProve that cos120∘cos240∘−sin120∘sin240∘=1
View SolutionProve that: cos3A+cos3(2π3+A)+cos3(4π3+A)=34cos3A
View SolutionProve that (sinA+cosA)(1−sinAcosA)=sin3A+cos3A
View Solution