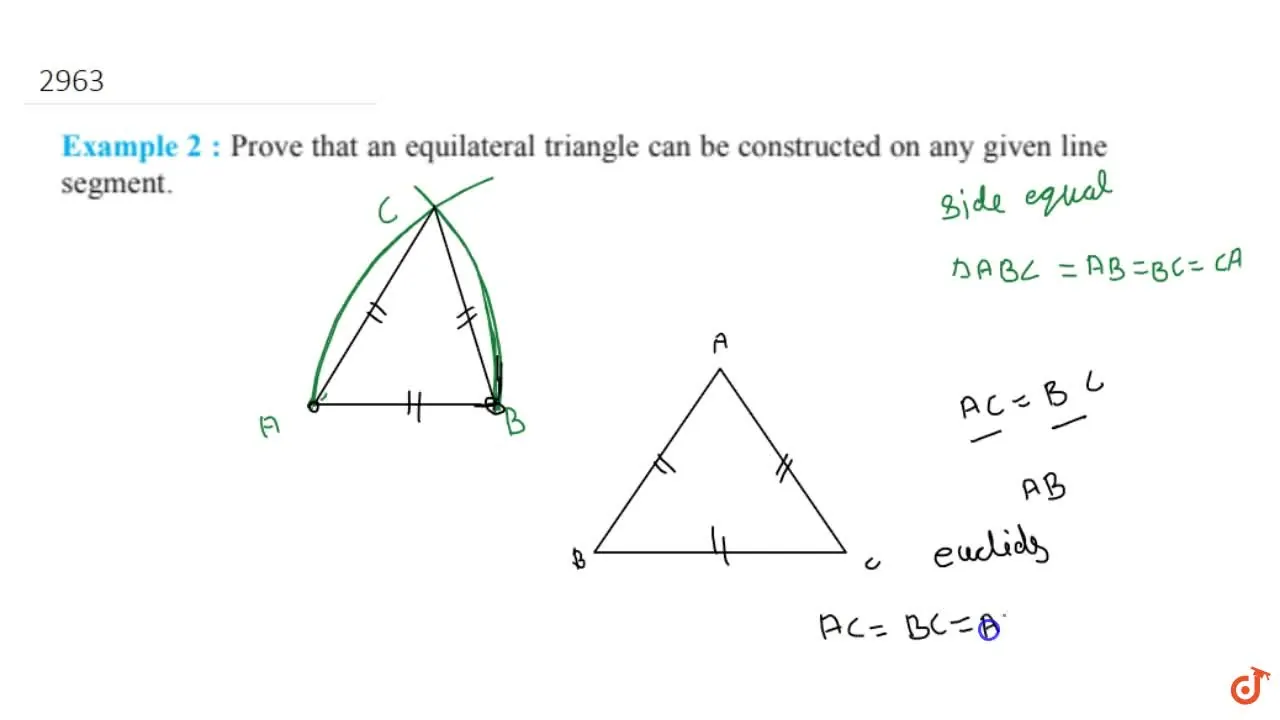
Prove that an equilateral triangle can be constructed on any given line segment.
First draw the line AB.
to draw a equilateral triangle
draw circles from both the points of the lineAB(remember that the radius of circle should equal to the length of lineAB)
the point where both the circles are intersecting, name that point C
after joining the points AC and BC
we get the required equilateral triangle.
Related Playlists
- BOOK - NCERTCHAPTER - INTRODUCTION TO EUCLIDS GEOMETRYEXERCISE - Exercise 5.22videos
INTRODUCTION TO EUCLIDS GEOMETRY
- BOOK - NCERTCHAPTER - HERONS FORMULAEXERCISE - Solved Examples6videos
HERONS FORMULA
- BOOK - NCERTCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - EXERCISE 4.42videos
LINEAR EQUATIONS IN TWO VARIABLES
Similar Questions
Prove that an equilateral triangle can be constracted on any given line segment
View SolutionProve that an equilateral triangle is equiangular.
View SolutionA triangle can be constructed by taking its sides as:
View SolutionProve that the medians of an equilateral triangle are equal.
View SolutionProve that area of an equilateral triangle formed on one side of a given square is one half of area of equilateral triangle formed on diagonal is the same square.
View SolutionA triangle can be constructed by taking two of its angles as:
View SolutionConstruct an equilateral triangle ABC of side 6cm.
View SolutionWith ruler and compasses, we can bisect any given line segment.
View SolutionProve that each angle of an equilateral triangle is 600
View SolutionProve that the area of equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonal.
View Solution